問題再設定:統計的因果探索問題
統計的因果推論問題の枠組みは、しばしば「統計的因果探索問題(Statistical Causal Discovery Problem)」の枠組みとして再設定される。実務上多くの場合、因果推論問題の解決策を展開しようとするモデル設計者たちは、事前知識や仮説が不足している状況に遭遇する。マーケティングにおける複数の施策と、売上高、顧客満足度、リピート率などといったKPIの達成状況との関連の中には、確かに因果関係が含まれているかもしれない。だが、KPIが複数個ある場合、あるいはKPIが定義されてすらいない場合、「原因変数」と「結果変数」の区別を導入することは困難となる。また、通常こうした施策とKPIの間には「原因」と「結果」によって「排除された第三項」が潜んでいる。こうした「反事実」上の「潜在的な結果」を取り扱うためには、データ駆動(data-driven)の探索が必要になる。
統計的因果探索問題は、因果関係のネットワーク構造をデータ駆動で探索していく問題である。その際、データ駆動型の探索の基盤となるのは、上述した構造方程式モデルやグラフィカルモデルである。
問題解決策:LiNGAM
Shimizu, S., et al. (2006)のLiNGAM(Linear Non-Gaussian Acyclic Model)は、統計的因果探索問題における最も早期に提案された解決策の一つである。LiNGAMはDAGを扱う線形構造方程式モデルを用いた因果探索のモデルとして知られている。ただしNon-Gaussianという形容表現にも表れている通り、この構造方程式モデルは誤差変数にガウス分布を仮定しない。誤差変数は相互に独立で、かつその分布は非ガウス連続分布となる。この誤差変数を$$e_i$$とするなら、LiNGAMのモデルは次のような構造方程式モデルとして記述できる。
$$x_i = \mu_i + \sum_{i \neq j} b_{ij}x_j + e_i$$
ここで、$$\mu_i$$は切片で、$$b_{ij}$$は係数を表わす。各変数$$x_i$$は、それ以外の変数$$x_j(j \neq i)$$と誤差変数$$e_i$$の線形結合によって計算される。誤差変数が相互に独立であるというのは、$$e_i (i=1, …, N)$$が、互いに独立であるということを意味する。このことは、どの観測変数の間にも潜在的な交絡因子となり得る「潜在変数(latent variable)」が存在しないという仮定を言い表しいる。
LiNGAMのモデルはDAGを想定している。例えば観測変数が$$x_1$$と$$x_2$$しか存在しない場合、因果の向きは$$x_1 \rightarrow x_2$$か$$x_1 \leftarrow x_2$$の二種類しか存在しない。この場合、LiNGAMのモデルも次の二種類の場合に分けることができる。
$$x_2 = e_2, \ x_1 = \mu_1 + b_{12}x_2 + e_1 (b_{12} \neq 0)$$
$$x_1 = e_1, \ x_2 = \mu_2 + b_{21}x_1 + e_2 (b_{21} \neq 0)$$
統計的因果探索問題を解決しようとしているモデル設計者は、与えられたデータセット$$X$$が、上記のどちらのモデルから生成されたのかがわからない。それは、$$x_1$$と$$x_2$$のどちらが最初に生成されたのかがわからないということでもある。そして無論、切片や誤差変数もわからない状況である。この時、モデル設計者は、$$X$$が上記のモデルのどちらから生成されたのかを、$$X$$のみから推定することになる。
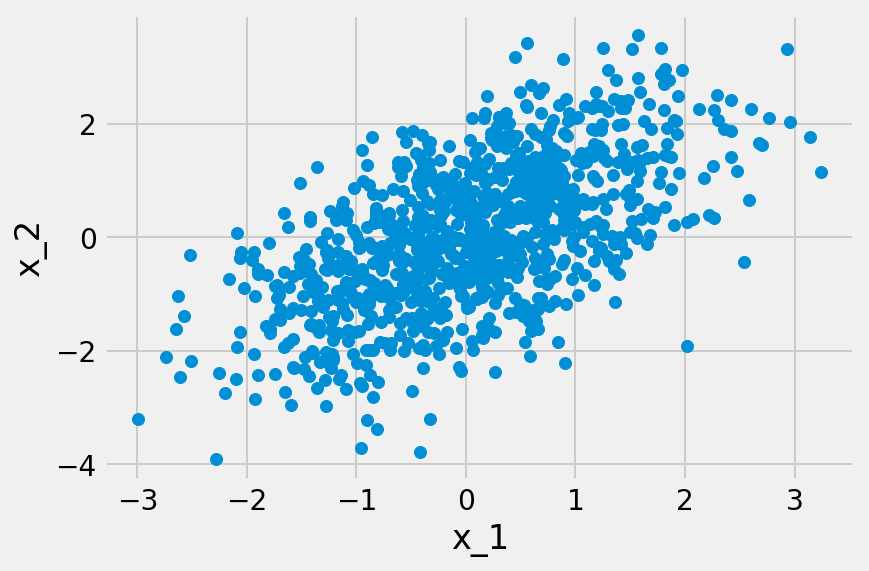
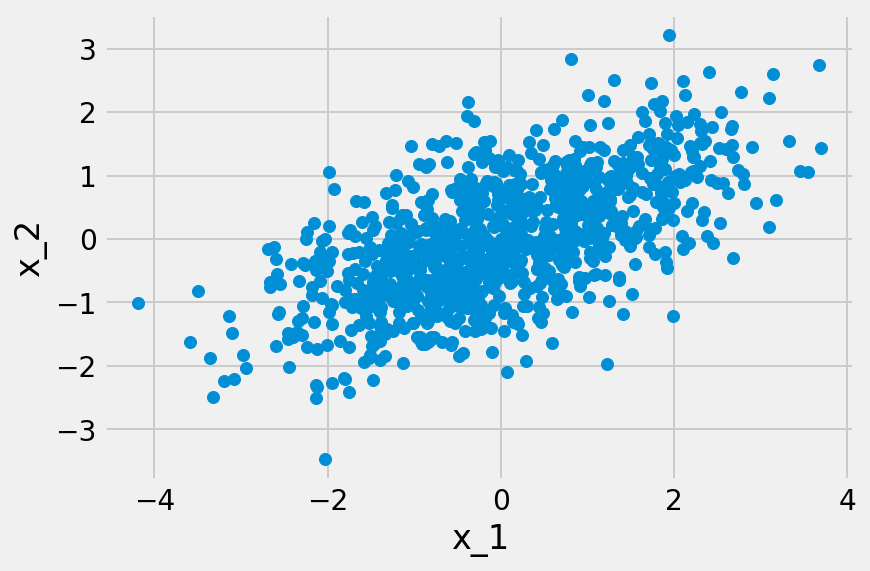
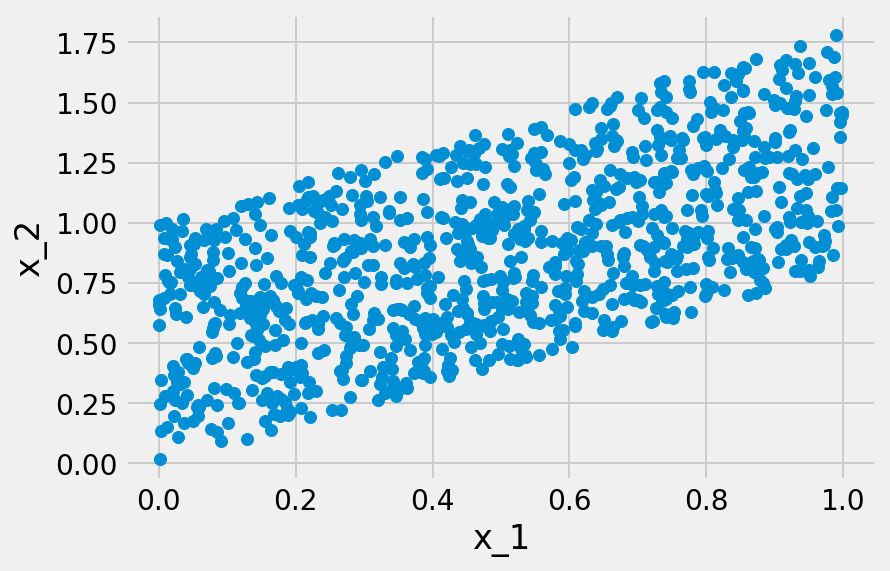
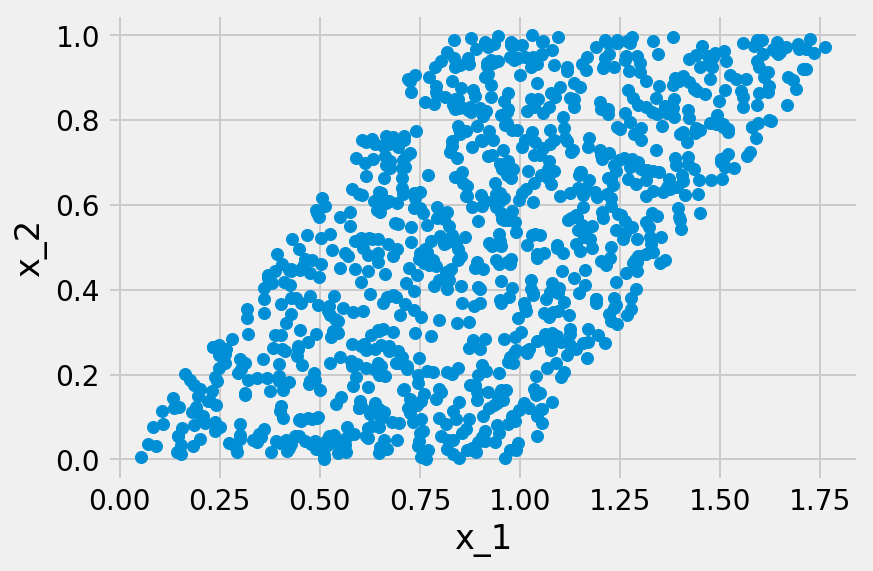
この推定を可能にする十分条件として知られているのが、LinGAMにおける二つの想定、つまり誤差変数が非ガウス分布に従うと共に、それが相互に独立であるという条件である。言い換えれば、この推定が可能であるためには、どの観測変数の間にも潜在的な交絡因子となり得る潜在変数が存在してはならないということになる。この潜在変数が存在しない場合、因果方向(causal direction)が異なる時に、データ分布も異なるためである。もし誤差変数がガウス分布に従っている場合、平均と分散共分散が規定されれば、分布も規定されてしまう。その結果、各観測変数の分布が同一になってしまう。そうなれば、因果の方向は区別できなくなる。
 |  |
 |  |
誤差変数$$e_i(i=1, …, N)$$が非ガウス分布に従い、かつ相互に独立であるという条件は、LiNGAMの推定を可能にしている。例えば$$x_1 = e_1$$で、$$x_2 = \mu_2 + b_{21}x_1 + e_2(b_{21} \neq 0)$$が真であるなら、$$x_1$$は「原因」で$$x_2$$が「結果」であるということになる。結果変数$$x_2$$を原因変数$$x_1$$に回帰させるなら、その残差$$r_2^{(1)}$$は次のようになる。
$$r_{21} = x_2 – \frac{cov[x_2, x_1]}{var[x_1]} x_1 = x_2 – b_{21}x_1 = e_2$$
ここで、$$cov[x_2, x_1]$$は$$x_2$$と$$x_1$$の共分散を、$$var[x_1]$$は$$x_1$$の分散を、それぞれ表わす。この$$r_{21} = e_2$$の関係を観れば、$$e_1$$と$$e_2$$は独立であるために、$$x_2$$から$$x_1 = e_1$$による影響を除去することが可能であることがわかる。つまり、$$x_1$$と$$r_{21}$$は独立になる。
逆に$$x_1$$を$$x_2$$に回帰させた場合、$$r_{12}$$は次のようになる。
$$r_{12} = x_1 – \frac{cov[x_1, x_2]}{var[x_2]}x_2 = \left\{1 – \frac{b_{21} cov[x_1, x_2]}{var[x_2]}\right\}e_1 -\frac{b_{21}var[x_1]}{var[x_2]}e_2$$
$$b_{21} \neq 0$$であるために、$$r_{12}$$は$$e_1$$のみならず$$e_2$$に依存して規定される。$$x_2$$の計算にも$$e_2$$が必要になる。そのため$$r_{12}$$と$$x_2$$は独立とはならない。
これを前提とするなら、真のモデルと等しい因果方向で回帰を実行した場合、観測変数と残差は独立になる。これに対し、新のモデルとは異なる因果方向で回帰を実行した場合は、観測変数と残差は独立とはならない。この差異は、観測変数に対して「原因」と「結果」の区別を導入しようとするモデル設計者に対し、有用な方向付けを与えている。観測変数と残差の独立性を確認すれば、想定していた原因変数と結果変数の組み合わせが真のモデルなのか否かを判断できる。それはつまり、真のモデルにおける因果方向を推定できるということである。
真の結果変数と真の原因変数で回帰を実行した場合に、観測変数と残差が独立になる。この条件が満たされるのは、あくまでも誤差変数が非ガウス連続分布に従っている場合である。ガウス連続分布では、無相関と独立が同値となる。そのため、観測変数と残差の独立性を推定することはできない。推定した因果方向が真であろうと偽であろうと、ガウス連続分布からサンプリングされている場合、観測変数と残差は無相関であり、独立となってしまうためである。
問題解決策:独立成分分析
LiNGAMの構造方程式モデルは、観測変数が外乱となる誤差変数の線形関数であって、その誤差変数が相互に独立している非ガウス分布に従うことを前提としている。この構造方程式モデルの前処理として$$x_i$$の平均を差し引くと、次の方程式が成り立つ。
$$\textbf{x} = \textbf{B}\textbf{x} + \textbf{e}$$
ここで、$$\textbf{B}$$は、変数の因果順序$$k(i)$$が既知ならば、行と列の置換により、厳密な下三角形に置換できる行列である(Bollen, K. A., 1989, pp80-81.)。下三角形というのは、対角線以上の要素が全て$$0$$になる構成になる。
$$\textbf{B} = \begin{pmatrix}
0 & 0 & 0 \\
b_{21} & 0 & 0 \\
b_{31} & b_{32} & 0
\end{pmatrix}$$
これは三つの観測変数を想定した構造方程式モデルの行列$$\textbf{B}$$である。この行列は構造方程式モデルにおける係数$$b_{lm}$$の機能的等価物である。つまりこの構造方程式モデルが言い表しているのは、$$x_2 \rightarrow x_1$$はあり得ても、$$x_1 \rightarrow x_2$$はあり得ないという非循環の有効グラフの関連なのである。この行列を前提とするなら、構造方程式モデルは次のように再記述できる。
$$\begin{pmatrix}
x_1\\
x_2 \\
x_3
\end{pmatrix} = \begin{pmatrix}
0 & 0 & 0 \\
b_{21} & 0 & 0 \\
b_{31} & b_{32} & 0
\end{pmatrix}\begin{pmatrix}
x_1 \\
x_2 \\
x_3
\end{pmatrix} + \begin{pmatrix}
e_1 \\
e_2 \\
e_3
\end{pmatrix}$$
単位行列を$$\textbf{I}$$とするなら、上述した方程式は次のように再記述できる。
$$\textbf{A} = (\textbf{I} – \textbf{B})^{-1}$$
$$\textbf{x} = \textbf{A}\textbf{e}$$
この$$\textbf{A}$$もまた、$$k(i)$$を参照することで、下三角形の行列を成す。尤も、この行列の場合は厳密な下三角形にはならない。実際には、対角要素が非ゼロとなり得る。いずれにせよこの方程式により、$$\textbf{x}$$を求めるにはまず$$\textbf{A}$$を求める必要があるということがわかる。この着眼点からShimizu, S., et al. (2006)は、$$\textbf{e}$$の独立性と非ガウス性を前提とすることで、このモデルが「独立成分分析(independent component analysis: ICA)」のモデルとして機能することを指摘している。
独立成分分析は「主成分分析(Principal Component Analysis: PCA)」を拡張させた多変量解析のモデルである。「主成分(principal component)」とは、相関のある多数の変数が、相関の無い少数の変数として表現された成分の集合を指す。その機能は主に、データの「次元削減(Dimensionality reduction, Dimension Reduction)」である。複合性の高いデータを扱う場合、計算コストが高く付く。そればかりか、モデルがデータに「過剰適合(overfitting)」するリスクが高まる。独立成分分析は、この主成分分析によって得られた主成分の線形変換により、この主成分間の関連を独立にするためのモデルである。この独立成分分析によって変換された主成分を特に「独立成分(independent components)」と呼ぶ。
独立成分分析は、$$\textbf{x} = \textbf{A}\textbf{e}$$によって得られる線形なモデルを特定するための統計的な技術として採用できる。ここでも重要な観点となるのが、非ガウス性である。データがガウス分布に従う場合、無相関と独立の区別が導入できなくなる。非ガウス性という性質は、独立成分分析でも利用される。そのため$$\textbf{x} = \textbf{A}\textbf{e}$$は、$$\textbf{x}$$が、独立な成分である$$\hat{\textbf{A}}$$と$$\textbf{e}$$に分解されたと考えることができる。
勿論、ここで得られる$$\hat{\textbf{A}}$$が$$\textbf{A} = (\textbf{I} – \textbf{B})^{-1}$$と一致するという保証は無い。と言うのも、独立成分分析による独立成分の抽出処理は、因果順序を想定して設計されている訳ではないためである。確かに、独立成分の順序を並び替え、それにより$$\textbf{A}$$の列を並び替え、データの確率密度が等価となるICAのモデルを得ることもできる。ICAを利用する場合、この順序の問題は些末であり、無視することができる。一方、LiNGAMでは、因果の正しい順序を発見しなければならない。ICAのモデルを得ることが、LiNGAMの構造方程式モデルを得ることに直結する訳ではないということは、留意しておく必要がある。
$$\hat{\textbf{A}}$$と$$\textbf{A} = (\textbf{I} – \textbf{B})^{-1}$$の間に差異が生じるもう一つの背景となるのは、独立成分のスケーリングに関わる問題だ。ICAのモデルでは、通常、全ての独立成分が単位分散の性質を持つと仮定される。この過程を満たすために、$$\hat{\textbf{A}}$$や$$\hat{\textbf{A}}^{-1}$$はスケーリングされなければならない。一方、LiNGAMの構造方程式モデルでは、誤差変数が任意の非ゼロとなる文さんを持つことを許容している。そのため、LiNGAMのモデリングをICAのモデリングに「寄せる」なら、まず$$\textbf{B}$$を計算する前段階として、全ての対角要素が$$1$$になるように$$\textbf{A}^{-1}$$の行を規格化(normalization)しておく必要がある。
総じて言えば、$$\hat{\textbf{A}} = \textbf{A} = (\textbf{I} – \textbf{B})^{-1}$$を成立させるためには、ICAのモデルとLiNGAMの構造方程式モデルのそれぞれに対して、変換処理を加える必要がある。ICAのモデルに対しては、因果順序を想定した$$\textbf{A}$$の要素を並び替え、というのはつまり、$$\textbf{B}$$の要素の並び替えを実行しなければならない。尤もこの並び替えの処理に関しては、誤差変数との兼ね合いによって、言うなれば「帳尻合わせ」ができる。と言うのは、$$\textbf{e}$$の要素が$$e_1$$、$$e_2$$、$$e_3$$の順序から$$e_2$$、$$e_1$$、$$e_3$$の順序に並び替えたとしても、この誤差変数と対応する$$\textbf{A}$$の要素を並び替えれば、計算結果は変わらないためである。同様に、$$\textbf{A}$$の値を$$D(\in \mathbb{R})$$倍としたとしても、今度は$$\textbf{e}$$の値を$$\frac{1}{D}$$倍すれば、やはり計算結果は変わらない。要素順序の並び替えにしても、その値の規格化にしても、整合性を保つことはできる。
問題解決策:潜在変数型LiNGAM
LiNGAMのモデルは、潜在的な交絡因子となり得る潜在変数が存在する場合にも応用できる。潜在変数が$$K$$個存在する場合、それを$$f_1, …, f_K$$と表わす。この場合、LiNGAMのモデルは次のように記述できる。
$$x_i = \mu_i + \sum_{k=1}^{K} \lambda_{ik}f_k + \sum_{j \neq i}^{} b_{ij} x_j + e_i$$
このように潜在変数が組み込まれたLiNGAMは特に「潜在変数型LiNGAM(latent variable LiNGAM: lvLiNGAM)」と呼ぶ(Hoyer, P. O., et al., 2008)。ここで、$$f_1, …, f_K$$は非ガウス分布に従い、かつ相互に独立すると仮定される。この仮定は、観測変数と潜在変数の区別を再帰的に導入することで、正当な仮定として扱われている。LiNGAMのモデリングにおいては、全ての変数は観測変数で、それ以外は誤差変数として記述される。この観測変数と誤差変数の区別を前提とするなら、潜在変数はこの区別によって「排除された第三項」として潜在化していることになる。だが、非ガウス性や独立性の点において、潜在変数は誤差変数と共通している。そこでlvLiNGAMのモデリングにおいては、あえてこの誤差変数を潜在変数として再記述する。つまり$$f_i := e_i$$として定義することにより、従来のLiNGAMのモデルに潜在変数を導入することを可能にしている。
初期のlvLiNGAMのモデリングにおいては、あらゆる潜在変数$$f_1, …, f_k$$を網羅的に記述することで、最尤推定やベイズ推定を実行する手法が採用された。しかし、モデル設計者たる人間にとって、潜在変数の全てを特定するのは実務上困難である。データから潜在変数の数を推定するのは困難極まりない。そこでShimizu, S., & Bollen, K. (2014)は、別様のモデリングを考案した。
LiNGAMにおける当初の構造方程式モデルは、次のように記述されていた。
$$x_i = \mu_i + \sum_{i \neq j} b_{ij}x_j + e_i$$
しかし、この構造方程式モデルはDAGに照応したモデルである。因果方向は有効グラフによって指し示されているはずだ。仮に$$x_i \leftarrow x_j$$の因果方向が真であるなら、その因果順序(causal orderings)に逆は無い。したがって、上記の構造方程式モデルは次のように再記述できる(Hoyer, P. O., et al., 2008, p367., Shimizu, S., & Bollen, K., 2014, p2635.)。
$$x_i = \mu_i + \sum_{k(j) \leq k(i)}^{}b_{ij}x_j + e_i$$
ここで、$$k(j) \leq k(i)$$は因果順序が$$i$$より$$j$$の方が先であることを意味し、$$x_i$$が$$x_j$$に依存して規定されていることを表わす。$$k(l)(l = 1, …, N)$$は、サンプルにおける全ての観測値において同一となる。観測値$$i$$に対する観測対象に固有の影響を想定するなら、非ガウス分布に従い、非循環で、線形の構造方程式モデルは、更に次のように定式化される。
$$x_l^{(i)} = \mu_l + \tilde{\mu}_l^{(i)} + \sum_{k(m) \leq k(l)}^{}b_{lm}x_m^{(i)} + e_l^{(i)}$$
このモデルと従来のLiNGAMとの差異は、個体に特化した効果$$\tilde{\mu}_l^{(i)}$$が導入されている点にある。$$\tilde{\mu}_l^{(i)}$$のパラメタは$$e_l^{(i)}$$と独立で、$$x_l^{(i)}$$と相関する。このことが意味するのは、観測値が識別可能なLiNGAMから生成され、恐らく$$\mu_l + \tilde{\mu}_l^{(i)}$$の異なるパラメタ値を使用することで生成されているということである。このモデルは、全ての観測値に共通する影響となる$$\mu_l$$と$$b_{lm}$$および、固有の特化した影響$$\tilde{\mu}_l^{(i)}$$を有している。この関連からShimizu, S., & Bollen, K. (2014)は、いわゆる「混合モデル(mixed models)」に因んで、このモデルを「混合LiNGAM(mixed-LiNGAM)」と呼ぶ。
Shimizu, S., & Bollen, K. (2014)の潜在変数を考慮したLiNGAMは、この混合LiNGAMと関わる。観測値$$i$$において、潜在変数が導入されたlvLiNGAMは次のようにモデル化される。
$$x_l^{(i)} = \mu_l + \sum_{k(m) \leq k(l)}^{} b_{lm}x_m^{(i)} + \sum_{q=1}^Q \lambda_{lq}f_q^{(i)} + e_l^{(i)}$$
上記の混合LiNGAMより、
$$\sum_{q=1}^Q \lambda_{lq}f_q^{(i)} = \tilde{\mu_l}^{(i)}$$
Hoyer, P. O., et al. (2008)のlvLiNGAMとは異なり、Shimizu, S., & Bollen, K. (2014)のlvLiNGAMは、交絡因子となり得る潜在変数$$f_q$$を明示的にモデル化してはいない。むしろShimizu, S., & Bollen, K. (2014)のlvLiNGAMは、単純にその総和となる$$\sum_{q=1}^Q \lambda_{lq}f_q^{(i)} = \tilde{\mu_l}^{(i)}$$を導入している。何故なら、Shimizu, S., & Bollen, K. (2014)のモデリングにおいて重要視されているのは、あくまで観測変数$$x_l$$における因果関係を推定することであって、潜在的な交絡因子$$f_q$$の関連を推定することではないためだ。そのためShimizu, S., & Bollen, K. (2014)は、$$\lambda_{lq}$$あるいは潜在的な交絡因子$$Q$$の個数は推定の対象外としている。この場合、構造方程式モデルの切片は、全ての観測値に共通する影響と観測に固有の影響の総和として表れるために、観測ごとに区別され得る。そして線形の場合、潜在的な交絡因子の影響が、この切片の差分として計算され得るということになる。
混合LiNGAMの推定において、Shimizu, S., & Bollen, K. (2014)はベイズ主義的な問題解決策を展開している。そのためにShimizu, S., & Bollen, K. (2014)は、誤差変数$$e_l$$の分布と、観測対象に固有の影響$$\mu_l^{(i)}$$を含むパラメタの事前分布をモデル化しようと試みている。一方、lvLiNGAMの推定では、やはり混合モデルの如く、観測対象に固有の切片$$\mu_l^{(i)}$$に事前分布を設定することで、ベイズ主義的なモデル選択を踏襲している。その際、事前分布の一例となるのは、ガウス分布である。上述した通り、観測対象に固有の切片は、複数の潜在的な交絡因子による影響の総和である。この観点からShimizu, S., & Bollen, K. (2014)は、中心極限定理に基づき、より多くの独立な変数の和がガウス分布に近付くことを念頭に置き、ベル型の分布を事前分布として採用することを提案している。
問題解決策:ベイジアンネットワーク
上述したベイジアンネットワークは、統計的因果探索問題の枠組みにおいても機能する問題解決策として知られている。LiNGAMの構造方程式モデルが連続変数を扱うのに対して、ベイジアンネットワークは離散変数や不等式による場合分けを扱う。ベイジアンネットワークによる因果探索は、多くの場合、先述した条件付き独立性の検定に基づいた半ば消去法的な取捨選択によって可能になる。この取捨選択により残存したノード間には依存関係もしくは条件付き依存関係が成立しているという前提から、関連のあるノード同士の因果関係の度合いが「条件付き確率表(Conditional Probability Table: CPT)」という形式で記述される。
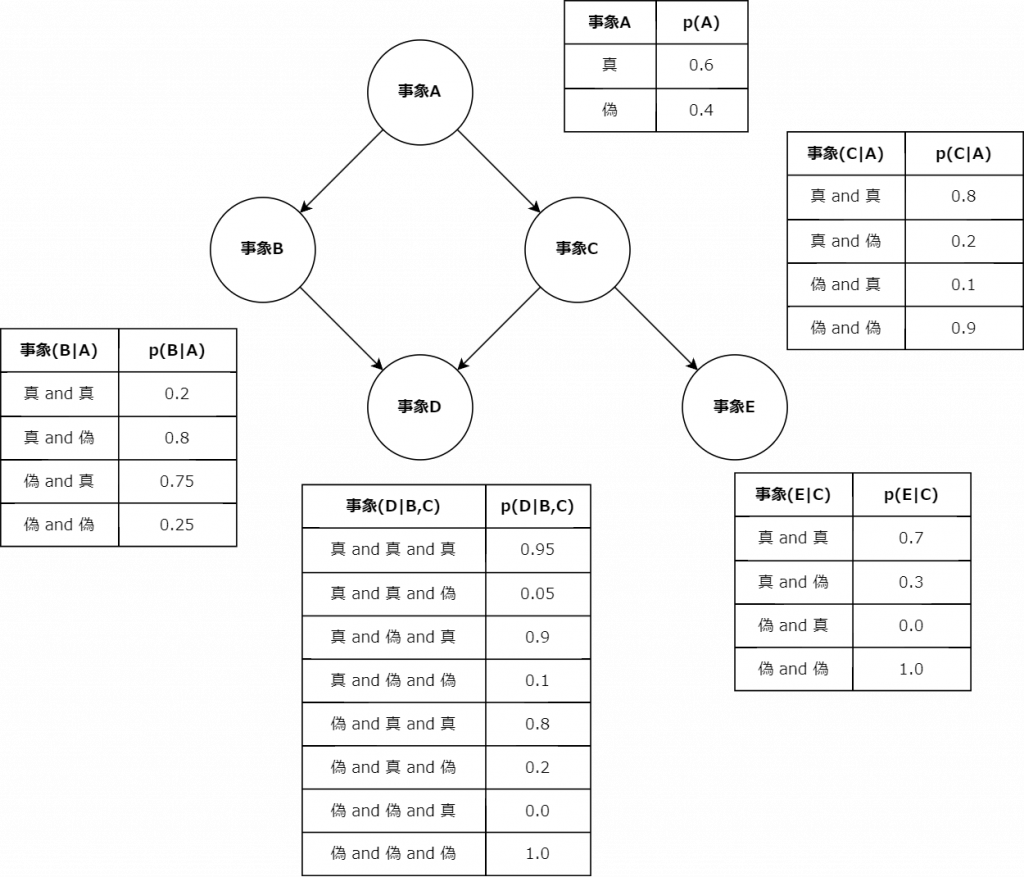 上図は、ベイジアンネットワークのネットワーク構造と条件付き確率表である。条件付き確率表の形式は、ネットワーク構造に応じて可変である。実務上は事象Dや事象Eのように、最も下流の事象と関わる確率のみを比較する場合もある。 |
ベイジアンネットワークの確率表の形式としては、条件付き確率を用いた条件付き確率表の他に、関連のある事象同士の同時確率分布を取り纏めた「同時確率分布表(Joint Probability Distribution Table: JPDT)」が採用される場合もある。ベイジアンネットワークを実務上応用される場合、CPTとJPDTは区別せず、「ファクター$$\phi$$(factor $$\phi$$)」と呼ばれることもある。変数集合$$\textbf{X}$$のファクター$$\phi$$は、変数集合$$\textbf{X}$$の各値$$\textbf{x}$$を非負値に写像させる関数で、特に$$\phi(\textbf{x})$$と表記する。
情報量基準を採用することの誤り
このファクター$$\phi$$を計算するためには、事前にベイジアンネットワークのネットワーク構造$$G$$をデータから推定する問題を解決しなければならない。統計学では、この問題は「モデル選択(model selection)」の問題として設定されている。モデル選択は元来、機能的に等価な問題解決策となり得る複数の統計モデルを選択することを意味する。そのためには、各モデルの性能を比較するための「相対的な評価量」(赤池弘次., 1996, p375.)が必要になる。一般的なモデル選択問題の枠組みでは、この比較の観点として、「情報量基準(An Information Criterion)」を最適化する場合のモデルが採用される。その代表的な指標として参照される傾向にある「赤池情報量規準(Akaike’s Information Criterion: AIC)」(Akaike, H., 1973)は、最大対数尤度$$L$$と最尤推定したパラメタの個数$$k$$から次のように計算される。
$$AIC = -2\log L – 2k$$
モデル選択では、このAICの値が小さいほど良いモデルであるという想定の下で、選択すべきモデルが規定される。パラメタを増やせば、表現力が高まることで、対数尤度が高まる。だがその際、過剰適合や計算コストなどのような様々な派生問題が生じる。そのためモデル選択では、パラメタの数を増やすこと自体が損失として想定される。誤差や尤度が同程度ならば、パラメタの数は少ない方が良いというのが、このAICの設計思想となる。
AICの基礎にある情報量の概念は、その提唱者である赤池弘次も述べている通り、ルートヴィッヒ・ボルツマンの熱力学的エントロピーの概念によって基礎付けられている。それは、一つの確率分布から観て、もう一つの確率分布がどの程度離れているのかを測るために機能する。
> 「AICの導入により、ただひとつのモデルについての推定論、検定論の議論に集中していた伝統的な統計学の枠組を超えて、さまざまな科学的研究の現場で、新しい統計モデルの提案と比較検討を通じて研究活動の推進が試みられるようになった。」
> 赤池弘次. (1996). AIC と MDL と BIC. オペレーションズ・リサーチ, 41(7), 375-378., p375.
尤も、後にこの比較の観点としてのAICは、それ自体が比較の対象として観察されるようになった。例えば「ベイズ情報量基準(Bayesian information criterion)」(Schwarz, G., 1978)は、モデル選択における比較の観点として機能するという点では、AICの機能的等価物である。BICは、以下のように、サンプルサイズ$$n$$を考慮した値となる。
$$BIC = -2\log L – k \log n$$
BICの設計思想においては、サンプルサイズがモデルの性能に影響を与えるとされる。サンプルサイズが大きくなれば、それだけBICに対する影響度も増していく。同じくベイズ主義と縁のあるベイジアンネットワークのモデル設計者たちは、Schwarz, G., (1978)のBICを採用する場合が散見される。しかし、AICやBICのような情報量基準は、近似の際に正則性を仮定している(LaMont, C. H., & Wiggins, P. A., 2015)。ベイジアンネットワークに正則性は無い。そのためベイジアンネットワークのモデル選択にこうした情報量基準を用いるのは、厳密には誤りである。尤も、モデル選択をベイズ統計的に実践する場合、周辺尤度を最大化するネットワーク構造を発見すれば良い。BICは対数周辺尤度を一般化させた近似に照応する(鈴木譲, 植野真臣, 2016)。そのためこの場合のモデル選択問題は、ベイジアンネットワークのネットワーク構造における周辺尤度最大化問題として再設定できる。
パラメタ化
ベイジアンネットワークのネットワーク構造$$G$$の学習は、他の統計モデルと同様に、パラメタ化(parameterization)から始まる。$$N$$個の離散変数集合$$x = \{x_1, …, x_N\}$$における各変数は、$$r_i$$個の状態の中から一つの値を取る。変数$$x_i$$が値$$k$$を取る場合、$$x_i = k$$と表記する。$$y = j$$を所与とした場合の$$x = k$$の条件付き確率は$$p(x = k \mid y = j)$$とする。このネットワーク構造を前提とした場合、ベイジアンネットワークの同時確率分布は、条件付き確率と確率の連鎖規則(chain rule of probability)により、次のようになる。
$$p(x_1, …, x_N) = \prod_{i=1}^{N}p(x_i \mid x_1, …, x_{i-1})$$
ベイジアンネットワークの場合、更に$$G$$を所与としているため、上記の同時確率分布は次のように再記述できる。
$$p(x_1, …, x_N \mid G) = \prod_{i=1}^{N}p(x_i \mid \Pi_i, G)$$
ここで、$$\Pi_i \in \{x_1, …, x_{q_i}\}$$は変数$$i$$の$$q_i$$個から成る親ノード集合を表わす。この同時確率分布を想定した上で、$$G$$のモデリングは、パラメタ集合$$\Theta$$についての尤度を記述することになる。親変数集合が$$j$$番目のパターンを取った時、つまり$$\Pi_i = j$$の時に変数$$x_i = k$$を取る場合の条件付き確率のパラメタを$$\theta_{ijk}$$とするなら、条件付き確率のパラメタ集合$$\Theta$$は次のようになる。
$$\Theta = \{\theta_{ijk}\}, (i = 1, …, N, j = 1, …, q_i, k=1, …, r_i)$$
この$$\Theta$$を前提とすれば、ベイジアンネットワークは$$G$$と$$\Theta$$の組み合わせ$$(G, \Theta)$$として表現できる。データ$$\textbf{X}$$を所与とした場合のパラメタ集合$$\Theta$$についての尤度は、次のような多項分布(multinomial distribution)となる。
$$p(\textbf{X} \mid \Theta, G) = \prod_{i=i}^{N}\prod_{j=1}^{q_i}\frac{\left(\sum_{k=1}^{r_i}n_{ijk}\right)!}{\prod_{k=1}^{r_i}n_{ijk}!}\prod_{k=1}^{r_i}\theta_{ijk}^{n_{ijk}} \propto \prod_{i=1}^N\prod_{j=1}^{q_i}\prod_{k=1}^{r_i}\theta_{ijk}^{n_{ijk}}$$
ここで、$$n_{ijk}$$は、変数$$i$$の親ノード変数集合に$$j$$番目のパターンを取り、変数$$i$$に対して$$k$$番目の値を取った場合のそのデータ数を意味する。
事前分布
頻度主義的な統計モデルにおいては、パラメタは確率分布としては記述されない。パラメタはあくまで一個の値として推定される。これに対して、ベイズ主義的な統計モデル、あるいは俗に言うベイズ統計学(Bayesian statistics)においては、パラメタは確率変数であって、推定したいパラメタは確率分布として表現される。
ベイズ統計は「ベイズの定理(Bayes’ theorem)」を用いて推論を実践する統計学である。「ベイズの定理」は、ある事象$$x$$の確率を事前の知識に基づいて記述する定理である。
$$p(x \mid \textbf{Y}) = \frac{p(\textbf{Y} \mid x) p(x)}{\sum_x^{}p(\textbf{Y} \mid x)p(x)} \propto p(\textbf{Y} \mid x) p(x)$$
ここで、$$p(x \mid \textbf{Y})$$の条件付き分布は特に「事後分布(posterior distribution)」と呼ぶ。$$p(\textbf{Y} \mid x)$$は、$$x$$の値を所与とした場合にデータ$$\textbf{Y}$$が観測される確率で、尤度に相当する。また$$p(x)$$はデータ$$\textbf{Y}$$を所与としない場合の$$x$$の確率分布で、特に「事前分布(prior distribution)」と呼ぶ。「ベイズの定理」が言い表しているのは、事後分布が尤度と事前分布の積に比例するということである。この確率分布の性質を利用した推定法を「ベイズ推定(Bayesian estimation)」と呼ぶ。
ベイズ推定において肝となるのは事前分布の設定だ。ベイズ統計学的に言えば、事前分布を選択する方法は二つある。第一に、可能な限り十分な情報に準拠するという点で、「情報的(informative)な」方法だ。こうして設定された事前分布は、「情報的事前分布(informative prior)」と呼ばれる。だが「情報的事前分布」を利用する場合、人によっては、異なる背景知識や解釈に基づいて事前分布を決定してしまうことがある。そのためこの「情報的な」方法はしばしば「主観的」であるとして、批判されている。一方、第二の方法は、「非情報的(Non-informative)な」方法である。これは、可能な限り制約を課さずにデータそのものに事前分布を語らせようとする姿勢を意味する。こうして語られる事前分布は特に「非情報的事前分布(Non-informative prior)」と呼ばれる。
構造学習
ベイジアンネットワークのネットワーク構造$$G$$の学習は、この「情報的」と「非情報的」の区別を導入するベイズ推定によって可能になる。いずれの方法が採用されるのかは、モデル設計者の理念に左右される。だが情報的な方法を採用するということは、ネットワーク構造$$G$$についての事前知識が十分であるという前提に立たなければならない。この想定は、後述するように、モデル設計者によってはありそうもない想定と見做される場合もある。その際、より「非情報的な」方法が追究される傾向にある。
パラメタ$$\Theta$$についての事前分布を$$p(\Theta \mid G)$$を想定する場合、その事前分布の性質は、モデル設計者の事前信念やいわゆる「主観」に左右されてしまう。これに対してベイズ統計学では、この事前分布の設計に合理性を与えるために、特に「共役事前分布(conjecture prior)」を念頭に置く。共役事前分布とは、その事後分布が事前分布と同一の分布形状になるような事前分布である。以下の「ディレクレ分布(Dirichlet distribution)」は、上述した多項分布の共役事前分布として知られている。
$$p(\Theta \mid G) = \prod_{i=1}^N\prod_{j=1}^{q_i} \frac{\Gamma \left(\sum_{k=1}^{r_i}\alpha_{ijk}\right)}{\prod_{k=1}^{r_i}\Gamma (\alpha_{ijk})}\prod_{k=1}^{r_i}\theta_{ijk}^{\alpha_{ijk}-1}$$
ここで、$$\Gamma$$はガンマ関数で、$$\Gamma(x + 1) = x\Gamma(x)$$となる。$$\alpha_{ijk}$$はハイパーパラメタで、$$n_{ijk}$$に対応する事前知識を表現した「疑似サンプル(pseudo sample)」と呼ばれる。上述した多項分布の規格化項として機能している$$\frac{\left(\sum_{k=1}^{r_i}n_{ijk}\right)!}{\prod_{k=1}^{r_i}n_{ijk}!}$$を抜きにして観れば、このディレクレ分布と多項分布は類似した構造を形成していることがわかる。
パラメタ推定
「ベイズの定理」によれば、事後分布は事前分布と尤度を掛け合わせることで計算できる。ベイジアンネットワークの場合、上述した尤度とディレクレ分布により、次のような事後分布が計算される。
$$p(\textbf{X}, \Theta \mid G) = \prod_{i=1}^N\prod_{j=1}^{q_i}\frac{\Gamma\left(\sum_{k=1}^{r_i}\alpha_{ijk}\right)}{\prod_{k=1}^{r_i}\Gamma(\alpha_{ijk})}\prod_{k=1}^{r_i}\theta_{ijk}^{\alpha_{ijk} + n_{ijk} – 1} \propto \prod_{i=1}^N\prod_{j=1}^{q_i}\prod_{k=1}^{r_i}\theta_{ijk}^{\alpha_{ijk} + n_{ijk} – 1}$$
事後分布、尤度、事前分布の関連を観れば、ハイパーパラメタとして指定することになる$$\alpha_{ijk}$$は、データ数$$n_{ijk}$$によって加算されていることがわかる。言うなれば$$\alpha_{ijk}$$は、データを観測する前段階における$${ijk}$$に対応する事象の主観的な頻度なのである。尤も、$$\alpha_{ijk}$$は実数でも構わない。そのため、このハイパーパラメタが指し示しているのは、頻度という概念を、より情報量の高く、粒度の細かい指標として拡張した概念であると言える。
この事後分布の期待値は、加算されていく指標である$$\alpha_{ijk}$$を念頭に置くなら、単純に定式化することができる。
$$\bar{\theta}_{ijk} = \frac{\alpha_{ijk} + n_{ijk}}{\alpha_{ij} + n_{ij}}$$
ベイジアンネットワークの学習では、この事後分布の期待値を探索していくアルゴリズムとなる。
周辺尤度最大化
以上のようなパラメタ推定から、ベイジアンネットワークのネットワーク構造における周辺尤度を計算する手筈が整えられる。次のように、やはりハイパーパラメタ$$\alpha_{ijk}$$は欠かせない要素となる。
$$p(\textbf{X} \mid G) = \int_{\theta}^{} p(\textbf{X} \mid \theta, G)p(\theta)d\theta = \prod_{i=1}^{N}\prod_{j=1}^{q_i}\frac{\Gamma(\alpha_{ij})}{\Gamma(\alpha_{ij} + n_{ij})}\prod_{k=1}^{r_i}\frac{(\alpha_{ijk} + n_{ijk})}{\Gamma(\alpha_{ijk})}$$
ベイジアンネットワークにおける周辺尤度最大化問題は、ハイパーパラメタ$$\alpha_{ijk}$$は如何にして規定され得るのかという派生問題を生み出している。これに対してHeckerman, D., et al. (1995)は、「等価尤度の仮説(assumption of likelihood equivalence)」を導入している。「等価尤度の仮説」とは、二つの構造が等価であるのならば、それらのパラメタ同時確率密度は同一であるはずだという仮説である。例えば$$p(G_1 \mid \zeta) > 0$$かつ$$p(G_2 \mid \zeta) > 0$$となるような構造$$G_1$$と$$G_2$$が与えられ、この二つの構造が等価であるのならば、$$p(\Theta_{G_1} \mid G_1, \zeta) = p(\Theta_{G_2} \mid G_2, \zeta)$$となる。構造学習がこの条件を満たす場合、その結果は「尤度等価」の条件を満たしている。この関連からHeckerman, D., et al. (1995)は、「尤度等価」の条件を展開することで、ハイパーパラメタの和が一定となる条件を導入する。この条件を満たす計量は「ベイジアン-ディレクレ等価性(Bayesian Dirichlet equivalence: BDe)」の計量と呼ばれ、これにより、$$\alpha_{ijk}$$の特定が可能になるという。しかし、このBDeを計算するためには、「等価サンプルサイズ(equivalent sample size)」という事前知識の重み付けを担う別種のハイパーパラメタを指定する必要がある。この等価サンプルサイズを$$N’$$とするなら、$$\alpha_{ijk}$$は次のように計算される。
$$\alpha_{ijk} = N’ p(x_i = k, \Pi_i = j \mid G^h)$$
ここで、$$G^h$$はネットワーク構造の事前情報を反映させた仮説である。つまり$$\alpha_{ijk}$$は、ネットワーク構造に関するモデル設計者の事前信念によって規定されるという訳だ。しかし、モデル設計者が事前にある程度のネットワーク構造を理解できているというのは、ありそうもない状況である。そこでHeckerman, D., et al. (1995)は、Buntine, W. (1991)が提案している一様アサインメント(uninformative assignment)に基づく計量をBDeの特殊事例として採用している(Heckerman, D., et al. 1995, pp219-220.)。
$$\alpha_{ijk} = \frac{N’}{r_iq_i}$$
Heckerman, D., et al. (1995)はこの計量を特にBDeuと呼ぶ。このuは一様(uniform)のuである。実際、BDeuはパラメタの事前分布に一様分布を仮定しているために、純粋な無情報事前分布によって設計されている訳ではない。モデル設計者が十分な事前知識を持たない状態でBDeuを利用した場合、感度(sensitivity)により、事前分布の項が不安定または望ましくない結果になってしまう恐れがある。何故なら、事前分布は事前知識の欠如を表わすのではなく、条件付き分布の均一性に対する設計者の事前信念を表わすためだ。したがって、経験分布が歪んでいる場合、仮説の構造が真ではなくなるために、BDeuは等価サンプルサイズの値を小さくすることで事前信念の度合いを下げると想定される。一方これに対し、経験分布が一様である場合には、仮説の構造が真であるために、BDeuは等価サンプルサイズの値を大きくすることで事前信念の度合いを高めると考えられる。この結果、事前分布として一様分布を想定しているBDeuは非情報的事前分布を想定しているというよりは、むしろ条件付き分布の均一性に対する設計者の事前信念を想定していることになる(Ueno, M. 2012, p6.)。
それ故Ueno, M. (2012)は、この感度の問題を解決するために、NIP-BIC(non-informative prior Bayesian information criterion)という、よりロバスト性の高いスコアを提案している。
$$NIP-BIC = \sum_{i=1}^N\sum_{j=1}^{q_i}\sum_{k=1}^{r_i}(\alpha_{ijk} + n_{ijk})\log \frac{\alpha_{ijk} + n_{ijk}}{\alpha_{ij} + n_{ij}} – \frac{1}{2} q_i r_i \log (1 + n)$$
Ueno, M. (2012)によれば、NIP-BICはBDeuに比して、より高い性能改善の効果をもたらすという。何故なら、偏った分布と一様な分布を組み合わせたネットワーク構造を学習する上で、BDeuの$$N’$$の近似値を設定することは極めて困難となるためだ。ベイジアンネットワークのネットワーク構造は、通常、まさに歪んだ分布と一様な分布の組み合わせによって構成されている。この近似値の問題を回避できるというのは、NIP-BICの大きな利点となる。
条件付き独立性検定
ネットワーク構造$$G$$のモデル選択は、複数のモデルからの選択となる。BDeuやNIP-BICのような指標は、モデルの相対評価を可能にする。この相対評価によってより良き$$G$$を探索する方法は、「スコア準拠の構造学習(score-based structure learning)」と呼ばれている。多くの場合、この方法における構造学習では、未知の隣接行列$$A$$と観測データ点のサンプルに関する「スコア関数(score function)」として、BDeuやNIP-BICのような指標を利用する。$$G$$はDAGでなければならないというのは、$$A$$の構造上の制約条件ではある。だが$$G$$のモデル選択においては、選択肢を絞り込んでくれるという点で、この制約条件は有用である。
しかし、グラフのノードの個数が増えれば、ネットワークの複合性は指数関数的に増大していく。それは、$$G$$の候補が無数に、そして別様にもあり得るということである。モデルの選択肢が大量にあり得る場合、BDeuやNIP-BICを算出するための計算コストが高まる。そのためベイジアンネットワークの構造学習では、事前にモデル選択の選択肢を減らしておくことが求められる。その具体的な負担軽減策として採用されるのは、統計学の旧くからある手法として知られる「独立性検定(independence-test)」である。
ベイジアンネットワークの構造学習における独立性検定の機能は、ノード間の関連に対して、「独立(independence)」と「依存(dependence)」の区別を導入することにある。もしノード間の関連が「独立」であると認められたのならば、少なからずその双方に因果関係は見受けられないと言えるようになる。この場合、ベイジアンネットワークの構造学習は、「依存」の関連にあるノード間でのみ探索すれば良い。独立性検定の手続きにより、モデル設計者は、因果探索範囲を狭めることが可能になる。
他の統計検定と同じように、独立性検定でも「帰無仮説(null hypothesis)」と「代替仮説(Alternative hypothesis)」の区別を導入する。もし事象$$x_1$$と事象$$x_2$$の独立性を検定する場合、帰無仮説$$H_0$$は「事象$$x_1$$と事象$$x_2$$は独立である」となる。独立性検定では、この仮説の妥当性をデータから検証していく。もし妥当ではない場合、帰無仮説$$H_0$$は棄却(reject)される。尤も、$$H_0$$を棄却できなかった場合であっても、帰無仮説が正しいという結論にはなり得ない。勿論、代替仮説が間違っているという結論にもならない。この場合、帰無仮説の妥当性についての判断は保留となる。「帰無仮説が妥当ではないのならば代替仮説は妥当である」という言明も、あるいはその対偶となる「代替仮説が妥当でなければ帰無仮説は妥当である」という言明も、統計検定では誤りとなる。
独立性検定では「カイ二乗統計量(chi-square statistic)」を計算することで、帰無仮説を検討していく。上記の帰無仮説$$H_0$$を仮定した場合と比較して、データから計算されるカイ二乗統計量が著しく大きくなれば、$$H_0$$は棄却される運びとなる。
カイ二乗統計量は「度数分布表(frequency distribution table)」から計算される。$$R \times C$$から構成される度数分布表を想定するなら、カイ二乗統計量$$\chi^2$$は次のように計算される。
$$\chi^2 = \sum_{i}^R\sum_j^C \frac{(n_{ij} – E_{ij})^2}{E_{ij}}$$
ここで、$$n_{ij}$$は度数分布表における$$j$$列目の$$i$$行目における度数を表わす。$$E_{ij}$$は$$j$$列目の$$i$$行目における「期待度数(expected frequency)」で、行要素の合計や列要素の合計の比率から逆算して期待される度数を意味する。度数分布表における$$i$$行目のデータの総数を$$n_i$$、$$j$$列目のデータの総数を$$n_j$$、全データの総数を$$N$$とするなら、期待度数は次のように計算できる。
$$E_{ij} = \frac{n_in_j}{N}$$
$$\chi^2$$の値は、度数分布表の$$R$$や$$C$$に比例する。度数分布表のサイズの異なる対象同士のカイ二乗統計量を比較することはできない。この調整のために設けられているのが、「自由度(degrees of freedom)」という概念である。頻度や確率というのは、全データの総数$$N$$が既知であるなら、最後の行や最後の列の値は、その他の行や列の値から計算することができる。そのため自由度$$DF$$は、例えば次のように計算される。
$$DF = (R – 1)(C – 1)$$
算出された$$\chi^2$$と$$DF$$は、「カイ二乗分布(chi-square distribution)」と照合される。カイ二乗分布とは、互いに独立で標準正規分布$$\mathcal{N}(0, 1)$$に従う$$k$$個の確率変数$$Z_1, …, Z_k$$を想定した場合に、自由度$$DF = k$$の$$\chi^2$$が従う確率分布である。
$$\chi^2 = \sum_{i}^k Z_{i}^2$$
自由度$$DF = k$$の時のカイ二乗分布の確率密度関数は次のようになる。
$$f(x;k) = \left\{\begin{array}{ll}\frac{1}{2^{\frac{k}{2}}\Gamma\left(\frac{k}{2}\right)}e^{\left(-\frac{x}{2}\right)}x^{\left(\frac{k}{2}-1\right)} & (0 \leq x)\\0 & (x \leq 0)\end{array}\right.$$
ただし、$$\Gamma$$はガンマ関数を表わす。これを前提とすれば、カイ二乗分布は次のように可視化できる。
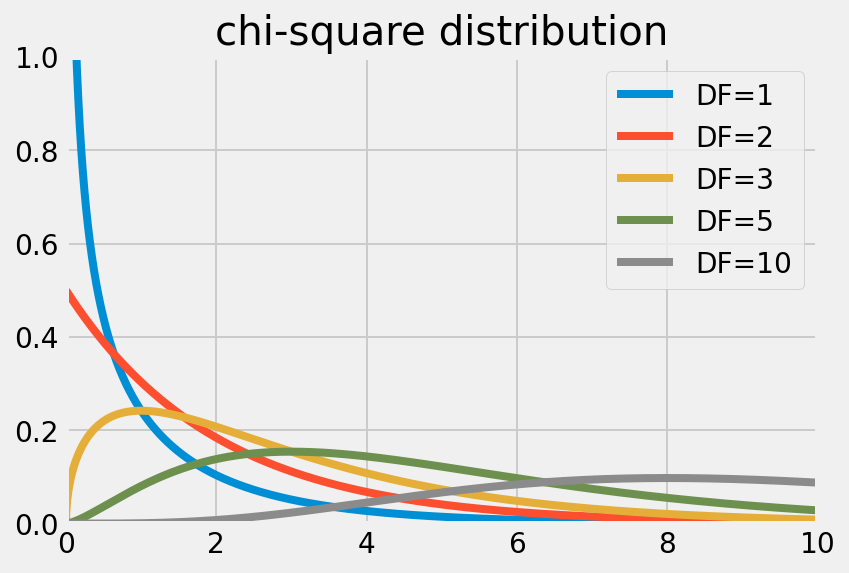 | 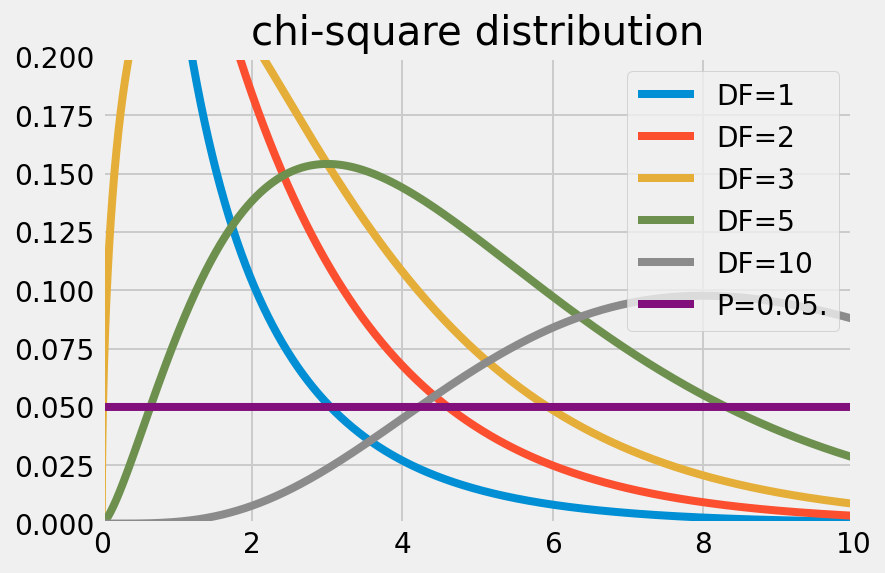 |
この分布が指し示しているのは、自由度$$DF$$を固定した上で、各事象間が独立である場合の$$\chi^2$$がどの程度ありそうもないことなのかである。独立性検定では、この確率の低いデータほど、独立性は低いと考えられる。その際、確率の低さ、ありそうもなさを判定する基準として設けられるのが、いわゆる「有意水準(Significance level)」だ。有意水準とは、帰無仮説を棄却する基準となる確率に他ならない。一般的には、有意水準$$P = 0.05$$が採用される。つまり、5%以下の確率でしか生起しないデータが得られた場合には、帰無仮説は棄却される。
ベイジアンネットワークの構造学習では、こうした帰無仮説を棄却する手続きにより、独立となるノード間の関連を因果探索範囲から除外していく。言わば消去法である。この手続きは、条件付き独立性を検定する場合においても、何ら変わらない。条件付き独立性を検定したい二つのノードを選択することで、それぞれの度数分布表から期待度数や自由度を算出する。そしてカイ二乗分布との照合から、事前に規定した有意水準を前提に、帰無仮説が棄却できるか否かを判断していく。因果推論問題の枠組みや因果探索問題の枠組みでは、この独立性の検定や条件付き独立性の検定によってネットワークの構造を学習していくアルゴリズムは、「PCアルゴリズム(PC algorithm)」(Spirtes, P., et al., 2000, pp84-122., Neapolitan, R. E., 2004, pp549-552.)という名称で認知されている。
参考文献
– Akaike, H. (1973). “Information theory and an extension of the maximum likelihood principle.” In B. N. Petrov and F. Csaki (Eds.), Second international symposium on information theory (pp. 267281). Budapest: Academiai Kiado.
– Akaike, H. (1974). A new look at the statistical model identification. IEEE transactions on automatic control, 19(6), 716-723.
– Akaike, H. (1981). Likelihood of a model and information criteria. Journal of econometrics, 16(1), 3-14.
– Biau, G., & Scornet, E. (2016). A random forest guided tour. Test, 25(2), 197-227.
– Blei, D. M., Ng, A. Y., & Jordan, M. I. (2003). Latent dirichlet allocation. Journal of machine Learning research, 3(Jan), 993-1022.
– Bollen, K. A. (1989). Structural equations with latent variables (Vol. 210). John Wiley & Sons.
– Breiman, L. (2001). Random forests. Machine learning, 45(1), 5-32.
– Bühlmann, P., Peters, J., & Ernest, J. (2014). CAM: Causal additive models, high-dimensional order search and penalized regression. The Annals of Statistics, 42(6), 2526-2556.
– Buntine, W. (1991). Theory refinement on Bayesian networks. In Uncertainty proceedings 1991 (pp. 52-60). Morgan Kaufmann.
– Cai, R., Xie, F., Glymour, C., Hao, Z., & Zhang, K. (2019). Triad constraints for learning causal structure of latent variables. Advances in neural information processing systems, 32.
– Cui, P., Wang, X., Pei, J., & Zhu, W. (2018). A survey on network embedding. IEEE transactions on knowledge and data engineering, 31(5), 833-852.
– Friedman, J. H. (2001). Greedy function approximation: a gradient boosting machine. Annals of statistics, 1189-1232.
– Glymour, M. M., & Greenland, S. (2008). Causal diagrams. Modern epidemiology, 3, 183-209.
– Goodfellow, I., Bengio, Y., & Courville, A. (2016). Deep learning. MIT press.
– Gretton, A., Bousquet, O., Smola, A., & Schölkopf, B. (2005, October). Measuring statistical dependence with Hilbert-Schmidt norms. In International conference on algorithmic learning theory (pp. 63-77). Springer, Berlin, Heidelberg.
– Gretton, A., Fukumizu, K., Teo, C., Song, L., Schölkopf, B., & Smola, A. (2007). A kernel statistical test of independence. Advances in neural information processing systems, 20.
– Grover, A., & Leskovec, J. (2016, August). node2vec: Scalable feature learning for networks. In Proceedings of the 22nd ACM SIGKDD international conference on Knowledge discovery and data mining (pp. 855-864).
– Heckerman, D., Geiger, D., & Chickering, D. M. (1995). Learning Bayesian networks: The combination of knowledge and statistical data. Machine learning, 20(3), 197-243.
– Heckerman, D. (2008). A tutorial on learning with Bayesian networks. Innovations in Bayesian networks, 33-82.
– Hoffman, M., Bach, F., & Blei, D. (2010). Online learning for latent dirichlet allocation. advances in neural information processing systems, 23.
– Hoffman, M. D., Blei, D. M., Wang, C., & Paisley, J. (2013). Stochastic variational inference. Journal of Machine Learning Research.
– Hoyer, P. O., Shimizu, S., Kerminen, A. J., & Palviainen, M. (2008). Estimation of causal effects using linear non-Gaussian causal models with hidden variables. International Journal of Approximate Reasoning, 49(2), 362-378.
– Hu, W., Zhang, C., Zhan, F., Zhang, L., & Wong, T. T. (2021, October). Conditional directed graph convolution for 3d human pose estimation. In Proceedings of the 29th ACM International Conference on Multimedia (pp. 602-611).
– Kalainathan, D. (2019). Generative neural networks to infer causal mechanisms: algorithms and applications (Doctoral dissertation, Université Paris Saclay (COmUE)).
– Kalainathan, D., Goudet, O., Guyon, I., Lopez-Paz, D., & Sebag, M. (2018). Structural agnostic modeling: Adversarial learning of causal graphs. arXiv preprint arXiv:1803.04929.
– Kipf, T. N., & Welling, M. (2016). Semi-supervised classification with graph convolutional networks. arXiv preprint arXiv:1609.02907.
– Koller, D., & Friedman, N. (2009). Probabilistic graphical models: principles and techniques. MIT press.
– LaMont, C. H., & Wiggins, P. A. (2015). Information-based inference for singular models and finite sample sizes: A frequentist information criterion. arXiv preprint arXiv:1506.05855.
– Neapolitan, R. E. (2004). Learning bayesian networks (Vol. 38). Upper Saddle River: Pearson Prentice Hall.
– Nowozin, S., Cseke, B., & Tomioka, R. (2016). f-gan: Training generative neural samplers using variational divergence minimization. Advances in neural information processing systems, 29.
– Maeda, T. N., & Shimizu, S. (2020, June). RCD: Repetitive causal discovery of linear non-Gaussian acyclic models with latent confounders. In International Conference on Artificial Intelligence and Statistics (pp. 735-745). PMLR.
– Maeda, T. N., & Shimizu, S. (2021, December). Causal additive models with unobserved variables. In Uncertainty in Artificial Intelligence (pp. 97-106). PMLR.
– Oprescu, M., Syrgkanis, V., & Wu, Z. S. (2019, May). Orthogonal random forest for causal inference. In International Conference on Machine Learning (pp. 4932-4941). PMLR.
– Pearl, J. (2003). Causality: models, reasoning, and inference. Econometric Theory, 19(675-685):46.
– Pearl, J. (2009). Causal inference in statistics: An overview. Statistics surveys, 3, 96-146.
– Perozzi, B., Al-Rfou, R., & Skiena, S. (2014, August). Deepwalk: Online learning of social representations. In Proceedings of the 20th ACM SIGKDD international conference on Knowledge discovery and data mining (pp. 701-710).
– Shimizu, S., Hoyer, P. O., Hyvärinen, A., Kerminen, A., & Jordan, M. (2006). A linear non-Gaussian acyclic model for causal discovery. Journal of Machine Learning Research, 7(10).
– Shimizu, S., & Bollen, K. (2014). Bayesian estimation of causal direction in acyclic structural equation models with individual-specific confounder variables and non-Gaussian distributions. J. Mach. Learn. Res., 15(1), 2629-2652.
– Spirtes, P. L., Meek, C., & Richardson, T. S. (2013). Causal inference in the presence of latent variables and selection bias. arXiv preprint arXiv:1302.4983.
– Spirtes, P., Glymour, C. N., Scheines, R., & Heckerman, D. (2000). Causation, prediction, and search. MIT press.
– Splawa-Neyman, J., Dabrowska, D. M., & Speed, T. P. (1990). On the application of probability theory to agricultural experiments. Essay on principles. Section 9. Statistical Science, 465-472.
– Rubin, D. B. (2005). Causal inference using potential outcomes: Design, modeling, decisions. Journal of the American Statistical Association, 100(469), 322-331.
– Schwarz, G. (1978). Estimating the dimension of a model. The annals of statistics, 461-464.
– Tong, Z., Liang, Y., Sun, C., Rosenblum, D. S., & Lim, A. (2020). Directed graph convolutional network. arXiv preprint arXiv:2004.13970.
– Ueno, M. (2012). Robust learning Bayesian networks for prior belief. arXiv preprint arXiv:1202.3766.
– Wager, S., & Athey, S. (2018). Estimation and inference of heterogeneous treatment effects using random forests. Journal of the American Statistical Association, 113(523), 1228-1242.
– Veličković, P., Cucurull, G., Casanova, A., Romero, A., Lio, P., & Bengio, Y. (2017). Graph attention networks. arXiv preprint arXiv:1710.10903.
– Yu, Y., Chen, J., Gao, T., & Yu, M. (2019, May). DAG-GNN: DAG structure learning with graph neural networks. In International Conference on Machine Learning (pp. 7154-7163). PMLR.
– Yuan, H., Yu, H., Gui, S., & Ji, S. (2020). Explainability in graph neural networks: A taxonomic survey. arXiv preprint arXiv:2012.15445.
– Zeng, Y., Shimizu, S., Cai, R., Xie, F., Yamamoto, M., & Hao, Z. (2021, December). Causal discovery with multi-domain LiNGAM for latent factors. In Causal Analysis Workshop Series (pp. 1-4). PMLR.
– Zheng, X., Aragam, B., Ravikumar, P. K., & Xing, E. P. (2018). Dags with no tears: Continuous optimization for structure learning. Advances in Neural Information Processing Systems, 31.
– 赤池弘次. (1996). AIC と MDL と BIC. オペレーションズ・リサーチ, 41(7), 375-378.
– 鈴木譲, 植野真臣(著)『確率的グラフィカルモデル』共立出版、2016
– 横井祥, 持橋大地, 高橋諒, 岡崎直観, & 乾健太郎. (2017). 独立性尺度に基づく知識の粒度の教師なし推定. In 人工知能学会全国大会論文集 第 31 回 (2017) (pp. 2B3OS07a1-2B3OS07a1). 一般社団法人 人工知能学会.