問題設定:ドメイン適応問題
『半教師あり学習による教師なしドメイン適応:深層再構成分類ネットワーク(DRCN)とPixelGANの機能』でも取り上げた通り、Bousmalis, K. et al.(2017)やWang, TC., et al. (2018)らの「敵対的生成ネットワーク(Generative Adversarial Networks: GAN)」の生成モデルを用いた「ドメイン適応(Domain Adaptation)」は、「教師なしドメイン適応」として位置付けられる。
「ドメイン適応(domain adaptation)」は転移学習の方法の一種として位置付けられている。ドメイン適応では、タスクと最適な入出力写像は各問題設定で同一であっても、それぞれの入力分布が微妙に異なっているような問題設定での転移学習を指す。これに対してドメイン適応のモデルは、ラベル付きサンプルが得られる「ソースドメイン(source domain)」と、ラベル付きサンプルが得られない、つまりラベル無しのサンプルしか得られない「ターゲットドメイン(target domain)」の区別を導入する。
GANによる教師なしドメイン適応は、ソースドメインにおけるラベル付きサンプルを条件付けGANのパラメタとして活用することで、ターゲットドメインにおけるラベル付きサンプルを生成することを可能にする。言い換えれば、GANによる教師なしドメイン適応は、min-maxの最適化に基づくターゲットドメインの擬似的なラベル付きサンプルを学習することを可能にする。
この生成モデルを再利用すれば、より少ないラベル付きサンプルから、擬似的なラベル付きサンプルを増やすことが可能になる。ラベル付け担当者が用意すべきラベル付きサンプルの量も、相対的に減らすことが可能になる。ソースドメインとターゲットドメインの区別は、N-Shot Learningにおける観測クラスと未観測クラスの区別と同様に、相対的な差異に基づいている。
ドメイン適応は、ソースドメインとターゲットドメインの区別を導入すると共に、ソースドメインの領域を徐々に拡張していくことにある。したがって、GANの生成モデルによる擬似的なラベル付きサンプルの生成処理は、理論的にはターゲットドメインにおける擬似的なラベル付きサンプルを生成していることになるものの、周り回ってソースドメインにおけるラベル付きサンプルを増やしていることに等しくなる。
問題解決策:PixelGANの機能
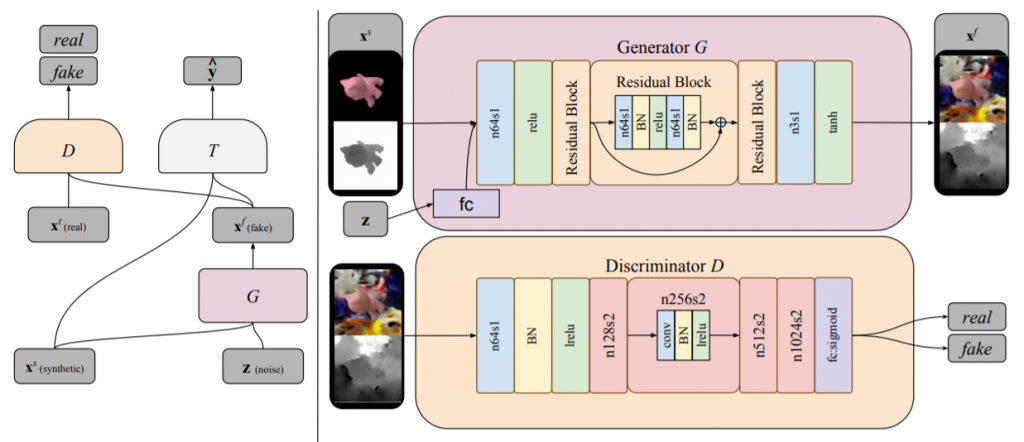
Bousmalis, K., Silberman, N., Dohan, D., Erhan, D., & Krishnan, D. (2017). Unsupervised pixel-level domain adaptation with generative adversarial networks. In Proceedings of the IEEE conference on computer vision and pattern recognition (pp. 3722-3731)., p3725より。
ターゲットドメインにおけるラベル付きサンプルを生成する生成器を$$G$$とする。訓練中、この生成器は $$G(x^s, z; \theta_G) \rightarrow x^f$$の特徴写像を実行する。ここで$$x^s$$はソースドメインにおけるサンプルを、$$z$$は入力ノイズのベクトルを、$$x^f$$は写像されたサンプルを、それぞれ表す。
一方、識別器$$D$$は、尤度$$d$$を出力する$$D(x; \theta_D)$$の関数として表現できる。ここでの$$x$$は、この識別器に入力されるターゲットドメインにおけるサンプルか、生成器によって写像された$$x^f$$である。識別器の機能は、このターゲットドメインにおける「真の」サンプルと生成器によって生成された擬似的なサンプルを識別することである。尚、データ分布に関しては、「真の」ソースドメインの分布を$$X^t$$、生成器の写像の分布を$$X^f$$とする。
通常の条件付きGANの構成に加えて、Bousmalis, K. et al.(2017)のドメイン適応用のGANでは、更に、識別器と生成器にとって正則項として機能する分類器$$T$$が追加される。これは$$T(x; \theta_T) \rightarrow \hat{y}$$で、$$\hat{y}$$は$$x \in \{X^f, X^t\}$$に対応するラベルを表す。
最適化は、次のmin-maxの最適化となる。
$$\min_{\theta_G, \theta_T} \max_{\theta_D} \alpha \mathcal{L}_d(D, G) + \beta \mathcal{L}_t(G, T) \tag{1}$$
ここで、$$\alpha$$と$$\beta$$は各誤差の重みを表すトレードオフのパラメタである。$$\mathcal{L}_d$$は次のようなドメイン誤差(domain loss)を表す。
$$\mathcal{L}_d(D, G) = \mathbb{E}_{x^t}[\log D(x^t; \theta_D)] + \mathbb{E}_{x^s, z}[\log (1 – D(G(x^s, z: \theta_G); \theta_D))] \tag{2}$$
また$$\mathcal{L}_t$$はタスク特化型誤差(task-specific loss)で、典型的な分類問題同様、クロスエントロピー誤差となる。
$$\mathcal{L}_t(G, T) = \mathbb{E}_{x^s, y^s, z}[-{y^s}^T \log T(G(x^s, z; \theta_G);\theta_T) – {y^s}^T \log T(x^s);\theta_T] \tag{3}$$
ここで、$$y^s$$はラベルを表現するone-hotなベクトルを、$$x^s$$はソースドメインにおけるサンプルを、それぞれ表す。
画像分類や映像分類、行動認識問題の枠組みで言えば、ソースドメインとターゲットドメインの差異が、画角の微小変化や、人間が位置する場所や時間、立ち位置、僅かな姿勢の傾き加減によって生じているのならば、Bousmalis, K. et al.(2017)のContent-similarity lossは有用な誤差関数となる。
$$\min_{\theta_G, \theta_T} \max_{\theta_D} \alpha \mathcal{L}_d(D, G) + \beta \mathcal{L}_t(G, T) + \gamma \mathcal{L}_c(G) \tag{4}$$
ここで、$$\gamma$$は$$\alpha$$や$$\beta$$と同じように、トレードオフのパラメタとなる。また$$\mathcal{L}_c(G)$$は次のようなmasked-PMSEとして計算される。
$$\mathcal{L}_c(G) = \mathbb{E}_{x^s, z}[\frac{1}{k} \mid \mid (x^s – G(x^s, z; \theta_G)) \circ m \mid \mid_2^2 – \frac{1}{k^2}((x^s – G(x^s, z; \theta_G))^T m)^2] \tag{5}$$
ここで、$$m$$は二値(0-1)のマスクとなる。$$k$$はピクセルの個数を表す。また$$\mid \mid \cdot \mid \mid_2^2$$はL2ノルムに他ならない。
機能的等価物:CrDoCo
PixelGANの半教師あり学習は、ラベル付きサンプルを生成することによって、ラベル付きサンプルの絶対量を増やす。この意味では、ラベル付きサンプルが少量であるが故に生じていたデータセットバイアスは、確かに解消へと向かうであろう。
しかし、式(2)が示すドメイン誤差の最小化を観るに、元々のソースドメインのラベル付きサンプルが偏っていた場合には、その影響が生成結果となるターゲットドメインの疑似的なラベル付きサンプルへも及ぶことがわかる。例えばソースドメイン内で完結したデータセットで汎化性能が得られないほど少量のデータセットを用いる場合には、このリスクは意識せざるを得なくなる。
あくまでもターゲットドメインにおける「真の」ラベル付きサンプルが得られない状況下で、このドメイン誤差最小化のリスクへの対処法として挙げられるのは、サンプルの表現学習を徹底することである。それは、単に特定のドメイン内のサンプルの表現学習に特化させるのではなく、ソースドメインとターゲットドメインの双方のサンプルの表現学習を徹底するということを意味する。
一つの補助線となるのは、Auto-Encoderの再構成誤差最小化問題であろう。この最小化問題では、符号化(encode)した特徴が良質な表現となっているか否かを、その復号化(decode)によって検証することになる。もし復号化した結果と元々の観測データ点との間の情報損失が少なければ、中間で埋め込まれている特徴点は、良質な表現となっていると期待できる。
Chen, Y. C., et al. (2019)が提唱しているCrDoCoは、この符号化と復号化の関連をソースドメインとターゲットドメインの関連へと転用したモデルであると見做すことができる。ドメイン誤差を最小化しようとする教師なしドメイン適応が、あるドメインのラベルなしサンプルを別のドメインのラベル付きサンプルへと変換していると見做すなら、この逆変換を検証することによって、当の変換の妥当性を評価することが可能になる。
教師なしドメイン適応の「クロスドメイン性」
このことを念頭に置いた上で、CrDoCoの定式化を確認してみよう。
ソースドメインのサンプルをターゲットドメインのサンプルへと変換する生成器と、その逆の返還を実行する生成器をそれぞれ$$G_{S \rightarrow T}, G_{T \rightarrow S}$$とする。これら二つのドメインのそれぞれのサンプル$$I_S, I_T$$を観測し、識別等の関心タスクに特化した深層アーキテクチャをそれぞれ$$F_S, F_T$$とする。この時、各生成器による変換は次のように表現できる。
$$I_{S \rightarrow T} = G_{S \rightarrow T}(I_S) \tag{1}$$
$$I_{T \rightarrow S} = G_{T \rightarrow S}(I_T) \tag{2}$$
これを前提とすれば、$$I_S, I_{T \rightarrow S}$$は$$F_S$$に入力され、$$I_T, I_{S \rightarrow T}$$は$$F_T$$に入力されることになる。
クロスドメイン一貫性誤差
この関連からChen, Y. C., et al. (2019)は、この双方向の変換の可能性から、CrDoCoの誤差関数の一種として設計されている「クロスドメイン一貫性誤差(Cross-domain consistency loss)」を記述することで、教師なしドメイン適応の「クロスドメイン性」に着目する。「真の」ラベル付きサンプルが得られないターゲットドメインのタスクを解決するためには、まずは式(2)より、ターゲットドメインのサンプルをソースドメインのサンプルに変換する必要がある。
ここで、Chen, Y. C., et al. (2019)の「鍵となる洞察(key insight)」となっているのは、$$I_T$$と$$I_{T \rightarrow S}$$は、異なる外観(appearance)や形状(styles)を持つかもしれないが、これら二つの画像が入力された深層アーキテクチャは、同一のタスク処理結果を出力するべきであると期待できる。言い換えれば、$$F_T(I_T) = F_S(I_{T \rightarrow S})$$が成り立たなければならない。
クロスドメイン一貫性誤差関数は、この二つのドメインの深層アーキテクチャ$$F_S, F_T$$の出力を橋渡しするように機能する。つまり、これら二つの出力の一貫性を担保するべく機能する。例えば、semantic segmentation taskを想定した場合、この誤差関数は次のような双方向のKLダイバージェンス(Kullback–Leibler divergence)によって設計される。
$$\mathcal{L}_{consis}(X_T; G_{S \rightarrow T}, G_{T \rightarrow S}, F_S, F_T) \\
= \ – \mathbb{E}_{I_T \sim X_T}\sum_{h,w,c}^{}f_{T \rightarrow S}(h, w, c)\log \left(f_T(h, w, c)\right) \\
\ \ – \mathbb{E}_{I_T \sim X_T}\sum_{h, w, c}^{}f_T(h,w,c)\log \left(f_{T \rightarrow S}(h,w,c)\right) \tag{3}$$
ここで、$$f_T = F_T(I_T), f_{T \rightarrow S} = F_S(I_{T \rightarrow S})$$はそれぞれ$$I_T, I_{T \rightarrow S}$$のタスクにおける予測結果を表す。また、cはクラス数を表す。
Chen, Y. C., et al. (2019)によれば、この誤差関数の設計は、あくまでsemantic segmentation taskを想定している。タスクが異なれば、この関数も異なる設計になる。例えばより深い予測タスクであれば、この誤差関数はL1ノルムの方が良い場合もあるという。
これ以外にもCrDoCoでは、タスク処理の結果に対する敵対的誤差を表す「特徴水準の敵対的誤差(Feature-level adversarial loss)」とクロスドメインに変換された画像同士の敵対的誤差を表す「画像水準の敵対的誤差(Image-level adversarial loss)」の区別が導入されている。いずれの誤差関数も、教師なしドメイン適応に備わっているクロスドメイン性に着目することで得られる発想だ。
機能的等価物:自己教師ありドメイン適応
『半教師あり学習による教師なしドメイン適応:深層再構成分類ネットワーク(DRCN)とPixelGANの機能』で取り上げた深層再構成分類ネットワーク(DRCN)とPixelGANとは異なり、J. Xu et al.の「自己教師ありドメイン適応(Self-Supervised Domain Adaptation)」は、「自己教師あり学習(Self-Supervised Learning)」によるドメイン適応を可能にしている。
一般的に自己教師あり学習の学習アルゴリズムは、本来解決したいタスクの前段階に実行される「プレテクストタスク(Pretext Task)」と当の解決したいタスクを表す「ダウンストリームタスク(Downstream tasks)」の二段階に区別される。多くの場合、後者の本来解決したいタスクは教師データやラベル付きサンプルが必要になる。これに対してプレテクストタスクでは、ラベルなしサンプルのみで可能になるラベルなし学習や最適化の手法が実行される。
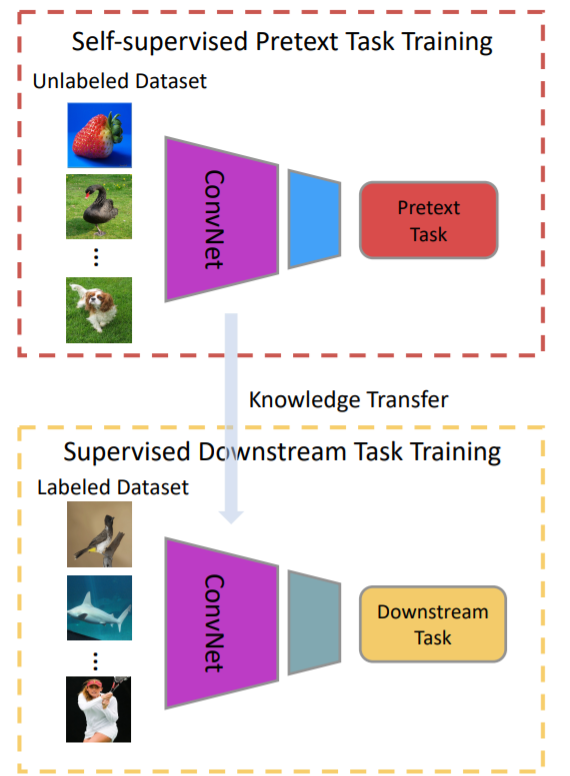
Jing, L., & Tian, Y. (2020). Self-supervised visual feature learning with deep neural networks: A survey. IEEE Transactions on Pattern Analysis and Machine Intelligence., p2.
半教師あり学習と自己教師あり学習の差異
自己教師あり学習は、2020年にはサーベイ論文(Jing, L., & Tian, Y., 2020)が提出されるほどに注目を集めているが、元々は人間によるラベル付けやアノテーションが必要であった教師あり学習の負担軽減策として考案されていた。特にプレテクストタスクの解決に資する教師なし学習のアルゴリズムは、ダウンストリームタスクの解決に必要となる表現学習や正則化として機能するために、相対的に少ないラベル付きサンプルでも精度向上を可能にする解決策として認知されていた。
半教師あり学習と同じように、自己教師あり学習もまた、ラベルなしサンプルを有効活用する。理論武装のみならず実務経験も蓄積している設計者ならば誰でも容易にわかることだが、どのような事業ドメインにおいても、ラベル付きサンプルはラベルなしサンプルよりも少量である。ラベル付きサンプルはヒューマンリソースを支払わなければ得られないためだ。このラベル付きサンプルとラベルなしサンプルの稀少性の格差に着目した「学習方法(learning methods)」が「半教師あり学習」であるのに対して、「自己教師あり学習」は同問題を解決するために機能する「教師なし学習の方法の集合(a subset of unsupervised learning methods)」として記述される傾向にある(Jing, L., & Tian, Y., 2020, p2.)。
このように記述すれば、半教師あり学習は自己教師あり学習を論理的に包含しているように視える。実際、両概念の差異は曖昧にも思える。この差異は、複合的な深層アーキテクチャのネットワーク構造(structure)、特にその概要のみを表す「図」を観るだけでは、到底把握できない。
しかし、それぞれの機能(function)を観察すれば、両者の比較は可能になる。つまり、半教師あり学習と自己教師あり学習が、それぞれどのような問題設定を前提としたどのような問題解決策として機能しているのかを観察すれば、その差異と同一性を区別することが可能になる。機械学習や統計的機械学習の場合、この機能的な比較の観点は、誤差関数(loss function)によって得られる。
構造(structure)から機能(function)へと視点を移すのではなく、関数(function)を機能(function)として分析することによって、半教師あり学習と自己教師あり学習の区別を導入することが可能になる。これは、『深層学習の企業内研究開発は「科学」なのか』で取り上げた機能的な分析方法によって比較の観点を導入することに等しい。
半教師あり学習の誤差関数
サンプル$$X_i$$、ラベル$$Y_i$$で構成された少量のラベル付きサンプルのデータセットXと、大量のラベルなしサンプルのデータセットZを想定するなら、N個の訓練データは
$$D_1 = \{X_i\}_{i=0}^N$$
となり、M個のラベルなしデータは
$$D2 = \{Z_i\}_{i=0}^M$$
となる。この時、一般的な半教師あり学習の誤差関数は、次のようになる。
$$loss(D1, D2) = \min_{\theta}\frac{1}{N}\sum_{i=1}^N loss(X_i, Y_i) + \frac{1}{M}\sum_{i=1}^M loss(Z_i, R(Z_i, X))$$
ここで、$$R(Z_i, X)$$はラベルなしサンプルのデータセットZとラベル付きサンプルのデータセットXとの関連を表現するtask-specificな関数を表す。
自己教師あり学習の誤差関数
一方、自己教師あり学習の誤差関数は、半教師あり学習とは異なる定式化によって導入される。N個の訓練データ集合$$D = \{P_i\}_{i=0}^N$$が与えられた時、誤差関数は次のようになる。
$$loss(D) = \min_{\theta}\frac{1}{N}\sum_{i=1}^Nloss(X_i, P_i)$$
疑似ラベルPが人間によるアノテーションなしに自動的に生成される場合、この関数は自己教師あり学習の誤差関数として機能する。自己教師あり学習においては、大量のデータセットに対するラベル付けやアノテーションの負担を軽減するために、一般的に深層アーキテクチャによって解決するためのプレテクストタスクが設計される。プレテクストタスクでは、疑似ラベルがデータの特徴に基づいて自動的に生成される。
自己教師ありドメイン適応のプレテクストタスク
J. Xu et al. (2019)の自己教師ありドメイン適応では、プレテクストタスクに画像回転予測(image rotation prediction)の問題設定が採用されている。モデルとして採用された畳み込みニューラルネットワークは、この問題設定の中で、画像の向きの予測を学習することにより、画像内の顕著な物体の位置を特定する。そしてこのモデルは、それらの向きと物体の型を認識することを、暗黙的に学習していく。
この暗黙的な認識は、ターゲットドメインにおける画像の意味論的な知識(semantic information)を含んでいる。この知識は、符号化器のネットワーク構造におけるクロスドメイン性の特徴表現力を向上させると期待される。言い換えれば、ターゲットドメインの画像を利用したプレテクストタスクは、符号化器がドメイン不変の特徴表現を学習する上で機能する。この機能があるからこそ、プレテクストタスクはドメイン適応の機能的等価物となり得るのである。
この機能的等価性を前提とすれば、確かにこの自己教師ありドメイン適応における符号化器部分のネットワーク構造は、『半教師あり学習による教師なしドメイン適応:深層再構成分類ネットワーク(DRCN)とPixelGANの機能』で取り上げた深層再構成分類ネットワーク(DRCN)における符号化器のネットワーク構造と類似している。いずれの符号化器も、本来解決したい問題の解決のために、ターゲットドメインのラベルなしサンプルを対象とした最適化を、交互学習のアルゴリズムの一環として実行している。
DRCNの符号化器の場合、ここでの最適化はAuto-Encoderの再構成誤差最小化であった。これに対してJ. Xu et al. (2019)のモデルでは、画像回転予測問題が採用されている。双方のネットワーク構造は、符号化器部分に派生の問題解決を担わせているという点で共通している。
しかしながら、自己教師ありドメイン適応のモデルはDRCNよりも幅広い問題設定の枠組みの中で設計されている。実際、J. Xu et al. (2019)はImageNetをはじめとした画像認識のノウハウを鵜呑みにしていない。ImageNetは画像の全体を認識しようとする。DRCNもまた、画像の全体の再構成誤差を最小化しようとする。しかし、特定のドメインからサンプルイングされた画像は、通常特定の構造やパターンに偏って生成されている。
この偏りの影響は、画像の全体を観測した場合にとりわけ深刻になる。画像の全体を利用した回転予測モデルで訓練した場合、訓練過程で明示的な解決策が発見される可能性があるものの、それ故にドメイン不変の特徴表現を学習する機会が喪われてしまう。それ故J. Xu et al. (2019)は、まず画像全体から画像パッチをアトランダムに抽出し、次にこのパッチを回転させるという手続きを採っている。こうして、プレテクストタスクの段階で、より複合的で多様なサンプルを学習することを可能にしている。
ドメイン適応の目的関数
ターゲットドメイン$$D_t = \{x_i^t\}_{i=0}^{N_t}$$から得られた$$N_t$$個の訓練画像の集合が与えられた時、幾何変換によって、0度、90度、180度、そして270度に回転させられた二次元画像の集合を定義することができる。$$g(x_i^t, r), \ r \in [0, 3]$$に基づく画像回転関数は、$$r \times 90$$の角度ごとに画像$$x_i^t$$を回転させる。この幾何変換の予測モデルPは、符号化器Eからの特徴写像を入力として受け取り、全ての可能な幾何変換に対する確率分布を出力する。
この時、自己教師あり学習は、この幾何変換のモデルが次の誤差関数を最小化するべく学習することになる。
$$\min_{\theta_e, \theta_p}\frac{1}{N_t}\sum_{i=1}^{N_t}\mathcal{L}_p(x_i^T, \theta_e, \theta_p) \tag{1}$$
ここで、$$\{\theta_e, \theta_p\}$$はそれぞれ符号化器Eとプレテクストタスクの深層アーキテクチャPのパラメタを表わす。また、
$$\mathcal{L}_p = – \frac{1}{4}\sum_{r=0}^{3}\log(P(E(g(x_i^t, r), \theta_e), \theta_p))\tag{2}$$
となる。
$$N_s$$個のラベル付きサンプルの画像がソースドメイン$$D_s = \{x_i^s, y_i^s\}_{i=0}^N$$から得られた時、セグメンテーションの深層アーキテクチャは、符号化器$$E(x_i^s)$$から得られた特徴写像を入力として受け取り、セグメンテーションの予測結果となる、$$\textbf{O}_i^s = S(E(x_i^s, \theta_e), \theta_s) \in \mathbb{R}^{H \times W \times C}$$を出力する。ここで、Cはセグメンテーションのカテゴリ数を表し、HとWはそれぞれ出力の縦幅と横幅を表す。$$\theta_e, \theta_s$$はそれぞれ符号化器とセグメンテーションタスクのモデルのパラメタを表す。EとSについて解くべきセグメンテーションの目的関数は次のようになる。
$$\min_{\theta_e, \theta_s}\frac{1}{N_s}\sum_{i=1}^{N_s}\mathcal{L}_{seg}(x_i^s, \theta_e, \theta_s) \tag{3}$$
ここで、セグメンテーションの誤差はクロスエントロピー誤差で、次のようになる。
$$\mathcal{L}_{seg} = – \sum_{h,w}^{}\sum_{c \in C}^{}y_i^s(h,w,c)\log(\textbf{O}_i^s(h,w,c))\tag{4}$$
(1)と(3)より、自己教師ありドメイン適応の目的関数は次のようになる。
$$\min_{\theta_e, \theta_p, \theta_s}\frac{1}{N_s}\sum_{i=1}^{N_s}\mathcal{L}_{seg}(x_i^s, \theta_e, \theta_s) + \frac{\lambda_p}{N_t}\sum_{j=1}^{N_t}\mathcal{L}_p(x_j^t, \theta_e, \theta_p) \tag{5}$$
ここで、$$\lambda_p$$は二つの誤差の均衡を制御する重みを表す。
自己教師ありドメイン適応の敵対的訓練
J. Xu et al. (2019)は、更なる精度向上のために、自己教師ありドメイン適応のモデルを敵対的生成ネットワークの構造へと拡張している。
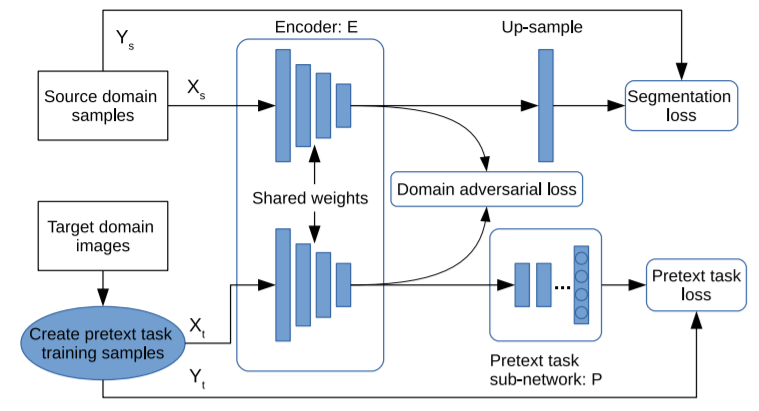
Xu, J., Xiao, L., & López, A. M. (2019). Self-supervised domain adaptation for computer vision tasks. IEEE Access, 7, 156694-156706., p156698.
このネットワーク構造では、先述した自己教師ありドメイン適応の構造に対して、復号化器(decoder)の層が追加されている。この層は、単純なup-samplingの層となる。また、符号化器(encoder)の最終層は予測の層に対応する。そして、予測の層の後にドメインの識別器(domain discriminator)を配置することにより、ドメイン敵対的訓練(domain adversarial training)が可能になる。
ここでいう識別器をパラメタ$$\theta_d$$を持つDと表記する。入力画像$$x_i$$が得られた時、この識別器は復号化器$$E(x_i)$$から得られた特徴写像を入力として受け取り、その特徴写像がソースドメインの写像なのかターゲットドメインの写像なのかを識別する二値分類を実行する。すなわち、$$\textbf{Z}_i = D(E(x_i)), \ \textbf{Z}_i \in \mathbb{R}^{H \times W \times 2}$$
Dの訓練は典型的な教師あり学習となる。それは次のような二次元のクロスエントロピー誤差の関数となる。
$$\mathcal{L}_d(x_i, \theta_d) = – \sum_{h, w}^{}[(1 – z)\log \textbf{Z}_i(h, w, 0) + z \log\textbf{Z}_i(h, w, 1)] \tag{6}$$
ここで、hとwはそれぞれ出力層の指数を表す。z = 0が指し示しているのは、そのサンプルがターゲットドメインからサンプリングされているということである。一方z = 1の場合はソースドメインからサンプリングされたことを表わす。
ドメイン不変の特徴表現を学習するために、符号化器にはDを欺けるようになって貰う必要がある。この敵対的ゲームは、次のような敵対的誤差の関数の最小化とアルゴリズム的に等価となる。
$$\mathcal{L}_{adv}(x_i, \theta_e) = – \sum_{h,w}^{}[(1 – z)\log \textbf{Z}_i(h, w, 1) + z \log \textbf{Z}_i(h, w, 0)] \tag{7}$$
この敵対的誤差がDを欺くべく$$\theta_e$$を最適化する一方で、式(6)の誤差関数は$$\theta_d$$の最適化によってDの分類精度を向上させる。一連の誤差の最小化が「ドメイン敵対的訓練」となるのは、式(6)と式(7)の最適化が競合しているためである。式(5)の自己教師ありドメイン適応の目的関数と組み合わせて再記述するなら、一連の最適化は次のようになる。
$$\min_{\theta_e, \theta_p, \theta_s, \theta_d}\frac{1}{N}\mathcal{L}_{seg}(x_i^s, \theta_e, \theta_s) \\ + \frac{\lambda_p}{N_t}\sum_{i=1}^{N_t}\mathcal{L}_p(x_i^t, \theta_e, \theta_p) \\ + \frac{\lambda_{adv}}{N_t}\sum_{i=1}^{N_t}\mathcal{L}_{adv}(x_i, \theta_e) \\ + \frac{\lambda_d}{N_t + N_s}\sum_{i=1}^{N_t + N_s}\mathcal{L}_d(x_i, \theta_d) \tag{8}$$
ここで、$$\lambda_{adv}, \lambda_{d}$$は各誤差の均衡を制御するパラメタを意味する。
補足
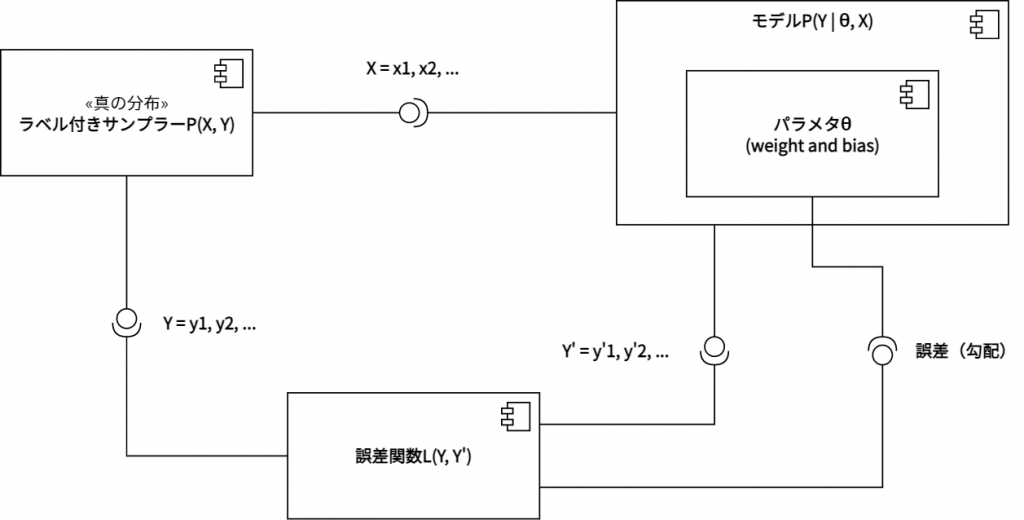
上図は、教師あり学習のコンポーネント図となる。ラベル付きサンプラーは、データ集合Xとこれに対応するラベル集合Yをサンプリングする。モデルPは、パラメタθとXの条件の下でYをサンプリングする。つまり入力Xとパラメタθにより、Y’を出力する。ラベル付きサンプラーとモデルPの出力は、誤差関数に入力される。これにより勾配が計算され、パラメタθへと逆伝播される。
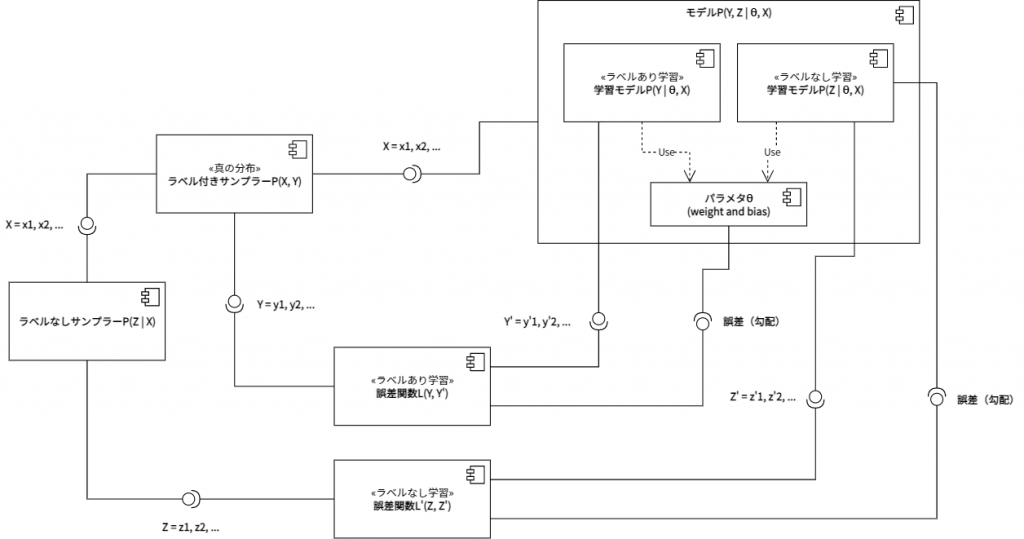
教師あり学習のコンポーネント図を半教師あり学習のコンポーネント図へと拡張すると、上図の通りとなる。ラベル付きサンプラーのサンプリング結果は、モデルPのみならずラベルなしサンプラーからも参照される。ラベルなしサンプラーは、このXに基づいて、ラベルなし学習における教師データZをサンプリングする。典型的な半教師あり学習は、このラベルなし学習を再構成誤差最小化問題として設定している。この場合、Z = Xとなる。一方、モデルPは入力XからY’とZ’を出力するように、パラメタθを配備している。これら二つの出力が、二つの誤差関数へと入力される。ラベルあり学習の誤差関数には、教師あり学習同様に、YとY’が入力される。ラベルなし学習の誤差関数には、ZとZ’が入力される。そしてそれぞれの誤差関数の出力が、モデルPのパラメタθへと逆伝播される。
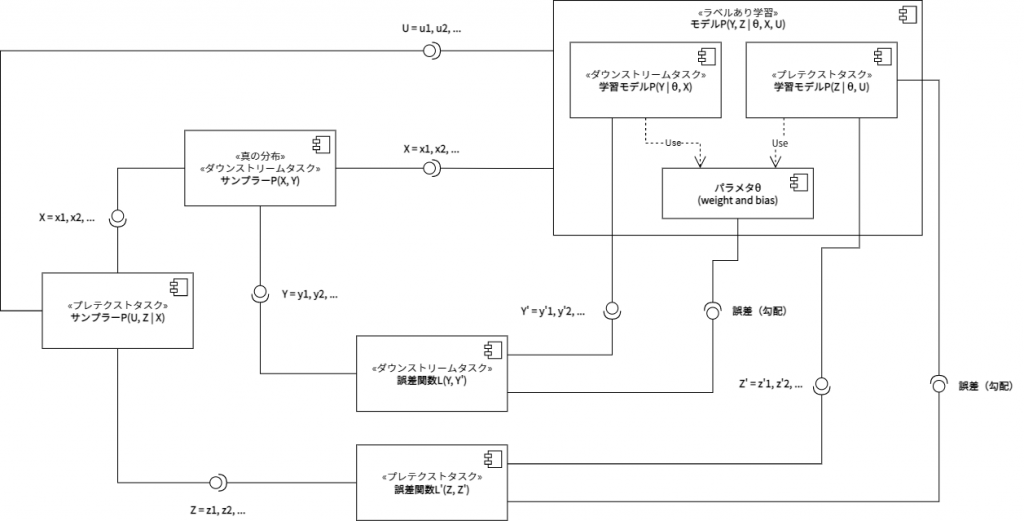
半教師あり学習のコンポーネント図を自己教師あり学習のコンポーネント図へと拡張すると、上図の通りとなる。「ラベルありサンプラー」と「ラベルなしサンプラー」の区別は、自己教師あり学習においては、「ダウンストリームタスクにおけるサンプラー」と「プレテクストタスクにおけるサンプラー」の区別として再記述される。「プレテクストタスクにおけるサンプラー」は、Xを変換するだけではなく、疑似的なラベルZも生成する。これにより、プレテクストタスクは疑似的な教師データを用いた教師あり学習として構造化される。また、「ラベルあり学習における誤差関数」と「ラベルなし学習における誤差関数」の区別は、やはり「ダウンストリームタスクにおける誤差関数」と「プレテクストタスクにおける誤差関数」の区別へと再記述される。一方モデルPは、「ダウンストリームタスクにおける学習モデルP」と「プレテクストタスクにおける学習モデルP」へと分化することになる。自己教師あり学習に特徴的なのは、ダウンストリームタスクとプレテクストタスクが、より明確に異なる入出力写像を学習しているということである。つまり、一方ではXとYの写像が、他方ではUとZの写像が学習される。これら二つの写像の学習は、やはり二つの誤差関数の逆伝播によって成り立っている。
参考文献
- Bousmalis, K., Silberman, N., Dohan, D., Erhan, D., & Krishnan, D. (2017). Unsupervised pixel-level domain adaptation with generative adversarial networks. In Proceedings of the IEEE conference on computer vision and pattern recognition (pp. 3722-3731).
- Chen, Y. C., Lin, Y. Y., Yang, M. H., & Huang, J. B. (2019). Crdoco: Pixel-level domain transfer with cross-domain consistency. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (pp. 1791-1800).
- Ghifary, M., Kleijn, W. B., Zhang, M., Balduzzi, D., & Li, W. (2016, October). Deep reconstruction-classification networks for unsupervised domain adaptation. In European Conference on Computer Vision (pp. 597-613). Springer, Cham.
- Glorot, X., Bordes, A., & Bengio, Y. (2011). Domain adaptation for large-scale sentiment classification: A deep learning approach. In Proceedings of the 28th international conference on machine learning (ICML-11) (pp. 513-520).
- Goodfellow, I., Bengio, Y., & Courville, A. (2016). Deep learning (adaptive computation and machine learning series). Adaptive Computation and Machine Learning series, 800.
- Jing, L., & Tian, Y. (2020). Self-supervised visual feature learning with deep neural networks: A survey. IEEE Transactions on Pattern Analysis and Machine Intelligence.
- Xu, J., Xiao, L., & López, A. M. (2019). Self-supervised domain adaptation for computer vision tasks. IEEE Access, 7, 156694-156706.