問題設定:GANにおける離散データの生成は如何にして可能になるのか
系列を生成する場合、GANのフレームワークは二つの問題を派生させる。
第一に、GANは実数値を生成するために設計されている点である。連続量のデータは、テキストのように離散化されたトークンの系列を直接的に生成する上で困難となる。何故ならGANのフレームワークにおいては、生成器がまずランダムサンプリングを開始してから、モデルのパラメタによって方向付けられた上で、決定論的な変換を実行するためである。
このようなアルゴリズムの場合、生成器による出力に関する識別器における損失(loss)の勾配は、生成される値をより現実味のある値へと微小に変異させていくように生成モデルを方向付けるために利用される。もし生成データが離散化されたトークンであるなら、この生成器から得られる「微小な変異(slight change)」の方向付けは有用ではなくなっていく。何故なら、制約された辞書空間において、トークンとこの微小な変異との間に対応関係があると見做す道理は何も無いためである。
第二の問題は、GANが与えるのは、系列データが生成された時の全系列におけるスコアと損失に限られている点である。部分的な系列を生成する上では、全系列としての現在と未来のスコアの帳尻を合わせるのは、決して単純な問題ではない。
問題解決策:SeqGAN
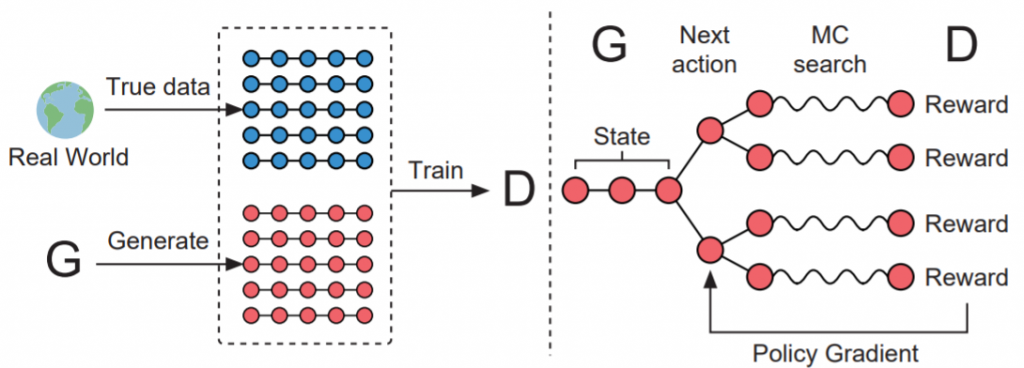
SeqGANは上記の問題を解決するために提案されたモデルである。このモデリングでは、系列データの生成がマルコフ過程に基づく時系列的な意思決定過程として記述される。生成モデルは強化学習におけるエージェントとして扱われる。状態は現時点で生成されたトークンに対応し、行動は次の時点に生成されるトークンに対応する。一方、識別器は系列を評価すると共に、その評価値をフィードバックすることで、生成モデルの学習を方向付ける。出力が離散的である場合に勾配が逆伝播され得ないという問題を解決するために、SeqGANのモデリングでは、生成モデルを確率的にパラメタ化された方策と見做す。この場合の勾配を特に「方策勾配(policy gradient)」と呼ぶ。
方策勾配の探索はモンテカルロ法によって実行される。この探索では、状態-行動価値観数の近似が可能になる。学習アルゴリズムは、方策としての生成モデルを方策勾配によって最適化することによって進行する。これによりSeqGANは、一般的なGANにおいて直面する離散データの微分困難を回避している。
『時系列的な意思決定としてのデータ生成』
系列データの生成を時系列的な意思決定として記述するというSeqGANの発想は、フィリップ・バチマンらの『時系列的な意思決定としてのデータ生成(Data generation as sequential decision making)』に由来している。データ生成問題を時系列的な意思決定問題として再設定した場合、この問題は強化学習アルゴリズムによって解決することが可能であるという着想が得られる。それは現時点のトークンから次の時点のトークンを選択する問題である。方策を方向付ける様々な報酬関数が、既に強化学習問題の枠組みから提供されている。
尤も、多くの報酬関数は全系列を観測した場合にのみ有意となる。こうした場合、状態-行動価値関数の評価はモンテカルロ法のような探索アルゴリズムによって実行される。一方、SeqGANのモデルでは、生成器を強化学習のエージェントとしてモデリングすることによって、系列生成問題を解決する。強化学習アルゴリズムによる探索では、全ての探索が終わる前から、ベルマン方程式を拡張させた再帰的なアルゴリズムによって、行動-価値関数の評価値を推定する。
SeqGANのモデル
θでパラメタ化された生成器を$$G_{\theta}$$とする。この生成器は系列 $$Y_{1:T} = (y_1, …, y_t, …, y_T), \ y_t \in \mathcal{Y}$$ を生成する。ここで、$$\mathcal{Y}$$は候補となるトークンの辞書を表す。時間幅をtとするなら、状態sは現在生成されているトークン $$(y_1, …, y_{t-1})$$を意味する。行動aは次に生成されるトークン $$y_t$$ となる。したがって、方策のモデル$$G_{\theta}(y_t \mid Y_{1:t-1})$$は確率的になる。行動が選択された直後の状態遷移は決定論的に実行される。
SeqGanにおける識別器は、Φでパラメタ化された識別機のモデルとして、$$D_{\phi}$$と表される。系列 $$Y_{1:T}$$が真の分布から得られた系列であるか否かを指し示す確率を$$D_{\phi}(Y_{1:T})$$と表す。この識別器が識別するのは、観測した系列データの真偽である。
GANのフレームワークの通り、生成器の学習は、識別器の結果に依存する。この原理は変わらない。だが生成器 $$G_{\theta}$$ は、識別器 $$D_{\phi}$$ から得られる最終的な報酬期待値を推定するモンテカルロ法によっても学習する。
Yu, L., Zhang, W., Wang, J., & Yu, Y. (2017, February). Seqgan: Sequence generative adversarial nets with policy gradient. In Thirty-First AAAI Conference on Artificial Intelligence., p2854.
方策勾配
方策勾配から学習する生成器 $$G_{\theta} (y_t \mid Y_{1:t-1})$$ は、最終的な報酬期待値の最大化のために学習していく。初期の状態を $$s_0$$ とするなら、
$$J(\theta) = \mathbb{E} [R_T \mid s_0, \theta ] = \sum_{y_1 \in \mathcal{Y}}^{} G_{\theta}(y_1 \mid s_0) \cdot Q_{D_{\phi}}^{G_{\theta}}(s_0, y_1)$$
となる。ここで、 $$R_T$$ は系列が完成した際の報酬を表す。注意しなければならないのは、前述した通り、ここでの報酬は識別器 $$D_{\phi}$$ から得られるということだ。 $$Q_{D_{\phi}}^{G_{\theta}}(s, a)$$ は系列の行動価値関数を表す。これは方策 $$G_{\theta}$$ に追従しつつ状態sから開始して行動aを選択していく場合に推定される累積報酬期待値を意味する。これを前提とするなら、生成モデルにおける目的関数は、識別器がそれを真の分布から得られた系列であると誤認してしまう系列を生成することを目標として設計されなければならない。
行動価値推定
行動価値推定は従来の強化学習アルゴリズムの方法によって実現する。しかし、識別器は最終系列における報酬値しか提供しない。報酬に対して長期的な展望を持つなら、各時間ステップにおいて、前時点までの全トークンのみならず、未来に得られるであろう結果も考慮しなければならない。それは、囲碁やチェス、将棋をはじめとしたゲームの戦略と同様である。プレイヤーはしばしば、最終的な勝利と戦況の長期的な展望のために、短期的な報酬を犠牲にすることがある。したがってSeqGANは、中間時点における行動価値を評価するために、未知の T – t のトークンを抽出する $$G_{\beta}$$ のロールアウト(roll-out)された方策をモンテカルロ法によって探索する。N回のモンテカルロ法の探索は次のようになる。
$$\left \{Y_{1:T}^1, …, Y_{1:T}^N \right \} = MC^{G_{\beta}}(Y_{1:t}; N)$$
ここで、$$Y_{1:t}^n = (y_1, …, y_t)$$と$$Y_{t+1}^n$$は、ロールアウトされた方策 $$G_{\beta}$$ と現在の状態に準拠して抽出される。$$G_{\beta}$$ は生成器と同様に参照される。探索アルゴリズムでは、まず出力されたサンプルのバッチを得るために、N回の系列の最終時点まで現在の状態から出発させる。これによりロールアウトされた勾配を次のように計算していく。
$$
Q_{D_{\phi}}^{G_{\theta}}\left(s = Y_{1:t-1}, a= y_t \right) = \begin{cases}
\frac{1}{N}\sum_{n=1}^N D_{\phi}(Y_{1:T}^n), T_{1:T}^n \in MC^{G_{\beta}}(Y_{1:t}; N) & (for \ t 生成器としてのRNNと識別器としてのCNN
SeqGANの生成モデルには再帰的ニューラルネットワーク(Recurrent Neural Network: RNN)が採用されている。出力層の活性化関数にはソフトマックス関数が導入されている。学習アルゴリズムには逆伝播を時系列的に実行していく時間化されたバックプロパゲーション(Backpropagation through time: BPTT)が採用されている。長期的な伝播による勾配消失と勾配爆発を回避する上では、LSTMのようなセルの区別を導入することが推奨されている。
一方、SeqGanの識別器にはCNNが用いられている。このCNNが識別するのは系列の最終状態の真偽に他ならない。つまりこの識別器は、未完の系列を観測しないことになる。出力層はロジスティクス関数を用いた全結合層として設計されている。損失関数にはクロスエントロピーが採用されている。これは、真の分布による系列であると予測された確率の誤差を学習することを意味する。
参考文献
- Bachman, P., & Precup, D. (2015). Data generation as sequential decision making. In Advances in Neural Information Processing Systems (pp. 3249-3257).
- Yu, L., Zhang, W., Wang, J., & Yu, Y. (2017, February). Seqgan: Sequence generative adversarial nets with policy gradient. In Thirty-First AAAI Conference on Artificial Intelligence.