異常検知問題における敵対的生成ネットワーク（GAN）の機能

問題設定：EncDec-AD以降の異常検知問題

異常検知問題は、コンピュータビジョンや動画認識の古典的な問題として参照されている。異常検知のモデルに求められる機能は、「異常な」データを「正常な」データから区別することである。そのためこの問題は、教師ありの識別問題として設定することも可能だ。しかし、データセットに偏り(bias)が含まれている場合、識別モデルは無力と化す。またこの識別問題の解決策を展開するためには、そもそも大量のラベル付きサンプルが必要になる。アノテーションには甚大なコストが生じる。

これに対してEncDec-ADのパラダイムは、異常検知問題を自己符号化器(Auto-Encoder)やEncoder/Decoderの再構成誤差最小化問題として再設定することで、ラベルなしサンプルの学習による異常検知を可能にした。しかしこのパラダイムに閉じ籠る場合、半教師あり学習へと結び付く多くの選択肢を手放すことになる。自己符号化器(Auto-Encoder)やEncoder/Decoderのパラメタを更新し得るのは、結局は再構成誤差の逆伝播と幾つかの正則化戦略だけである。一方、敵対的生成ネットワーク(Generative Advarsarial Networks: GANs)を用いた異常検知は、特に自己符号化器の機能を再利用すると共に、半教師あり学習との接続を可能にしている。それにより、GANのフレームワークで構造化された異常検知モデルは、EncDec-ADのパラダイムだけでは採用できなかった多くの正則化の戦略を遂行することを可能にしている。

問題解決策：AnoGAN

Schlegl et al. (2017)はまず、生成器と識別器を同時に訓練する。識別器は生成器によって生成されたデータと真のデータを識別するように訓練される。単一のコスト関数で最適化する代わりに、ここでの学習では、それぞれのコストのナッシュ均衡が目指される。これにより生成器の表現力と特異性(specificity)を増大させていく一方で、真のデータと生成データの差異を見極める識別器の性能を高めていく。

AnoGANのネットワーク構造

Schlegl et al. (2017)の定式化を確認しておこう。a×bの画像サイズのM個の画像集合を$$I_m \in \mathbb{R}^{a \times b}, m = 1, 2, …, M$$と置く。個々の画像から、c × cのサイズのK個の二次元画像パッチ$$x_{k, m}$$をアトランダムにサンプリングすると、そこから得られるデータは、$$\vec{x} = x_{k, m} \in \mathcal{X}, k = 1, 2, …, K$$となる。訓練中、敵対的生成ネットワークは$$\mathcal{X}$$における多様体を学習していく。この多様体は訓練画像の変動性(variability)を表現している。テストになると、$$\{y_n, l_n\}, n = 1, 2, …, N$$がサンプリングされる。ここで、$$y_n$$は新しいテストデータJから抽出されたc × cの未観測画像(unseen images)を表す。一方$$l_n \in \{0, 1\}$$は、画像ごとの真のラベルを表す。このラベルは、特定の異常度の定義に基づいて、異常検知の性能を評価するために利用される。訓練中は用いられない。ラベルを用意すべきなのは、テストデータにおいてのみである。

Schlegl et al. (2017)のGANは、二つの敵対的モジュールとなる生成器Gと識別器Dによって構成される。Gは、潜在ベクトルzの写像G(z)を経由して、xの分布$$p_g$$を学習する。zは潜在空間$$\mathcal{Z}$$から一様にサンプリングされた一次元のベクトルである。生成器の機能は、この潜在ベクトルを「正常な」データを表している二次元の画像空間における多様体$$\mathcal{X}$$へと写像することとなる。画像を観測する都合上、ここでのGのネットワーク構造は、転置畳み込み(transposed convolution / strided convolutions)の演算を用いた深層畳み込みニューラルネットワークのそれに等しくなる。一方、Dは二次元画像を単一のスカラー値となる$$D(\cdot)$$へと写像する一般的な深層畳み込みニューラルネットワークとして構造化される。このスカラー値の出力は、Dが真のデータを生成データから識別できる確率に対応している。

GとDは次の価値関数Vによって、二人のミニマックスゲームとして最適化される。

$$\min_G \max_D V(D, G) = \mathbb{E}_{x \sim p_{data}(x)} [\log D(x)] + \mathbb{E}_{z \sim p_z(x)}[\log (1 – D(G(z)))]$$

AnoGANの誤差関数

GANの学習が完了した後は、生成器が$$G(z) = z \mapsto x$$の写像を学習している。この写像が言い表しているのは、潜在空間表現zが「正常な」画像xへと写像されているということである。しかし、GANそれ自体は、この逆写像となる$$\mu(x) = x \mapsto z$$を自動的に学習してはくれない。

この潜在空間は滑らかな遷移を持つ。この空間内で近傍の二点からサンプリングすると、視覚的には類似した二つの画像が生成される。ここで目指されるのは、クエリとなる画像xを得た際に、xに視覚的に最も類似している画像G(z)に対応する潜在空間におけるデータ点zを発見することである。xとG(z)の類似度は、クエリ画像が生成器の訓練に使用されたデータ分布$$p_g$$をどの程度捕捉し得るのかに依存する。最良のzを発見するためには、潜在空間分布$$\mathcal{Z}$$から$$z_1$$をアトランダムにサンプリングした上で、生成画像$$G(z_1)$$を取得する必要がある。

この関連からSchlegl et al. (2017)は、この生成画像$$G(z_1))$$に基づいて誤差関数を設計している。この誤差関数は、$$z_1$$の係数を更新するための勾配を提供することで、潜在空間$$z_2$$の位置を更新することを可能にする。最も類似した画像$$G(z_{\Gamma})$$を発見するために、潜在空間$$\mathcal{Z}$$における位置zは、逆伝播のステップ$$\mathcal{r} = 1, 2, …, \Gamma$$の反復過程において最適化される。

Yeh, R., et al. (2016)に倣い、Schlegl et al. (2017)は「残差誤差(residual loss)」と「識別誤差(discrimination loss)」の区別を導入している。残差誤差$$\mathcal{L}_R(z_{\gamma}) = \sum_{}^{}\mid x – G(z_{\gamma})\mid$$は生成画像とクエリ画像の視覚的な類似度に基づいて計算される。生成器は、この誤差に従い、よりクエリ画像に類似した画像を生成するように方向付けられる。これに対して識別誤差$$\mathcal{L}_{\hat{D}}$$は、シグモイドクロスエントロピー(sigmoid cross entropy)の誤差として計算される。この誤差は、学習された多様体$$\mathcal{X}$$において、生成画像を生成画像として見抜けるか否かを表している。これら二つの誤差により、GとDは逆伝播を介してzの係数を適応させることが可能になる。

だがYeh, R., et al. (2016)の場合とは異なり、Schlegl et al. (2017)のAnoGANでは、$$z_{\gamma}$$が生成器によって出し抜かれた識別器の逆伝播で更新されることになる。そこでSchlegl et al. (2017)は識別誤差の代替案として、$$\mathcal{L}_D(z_{\gamma})$$を設計している。$$z_{\gamma}$$は、正常画像の分布の学習に伴って、あくまで$$G(z_{\gamma})$$と一致するように更新される。そこでSchlegl et al. (2017)は、GANの学習の安定化を可能にする特徴照合(feature matching)の技術に着目する。この技術では、生成器を最適化させるための目的関数が、GANの訓練を改善するように適合される。生成データに対する識別器の出力を最大化することによって生成器のパラメタを最適化する代わりに、生成器は訓練データと類似した特徴量を有する生成データ――言い換えれば、その特徴表現が実際の画像の特徴に類似する生成データ――を生成するように方向付けられる。

しばしば特徴照合は分類問題の性能改善においても有用であることが指摘される。しかしAnoGANの異常検知問題では、そもそも敵対的生成ネットワークの学習中にはラベル付けサンプルを参照しない。そのためSchlegl et al. (2017)は、ラベルに応じた識別的な特徴を学習するのではなく、良き表現学習を目指すことになる。つまり彼らは、潜在空間への写像を改善するために特徴照合を利用していくのである。

この関連から識別誤差$$\mathcal{L}_D$$はYeh, R., et al. (2016)の$$\mathcal{L}_{\hat{D}}$$から大きく逸脱していく。識別誤差の計算のために出力される識別誤差のスカラー値を利用する代わりに、Schlegl et al. (2017)は識別器の特徴表現を参照することで、次のように識別誤差を再定義する。

$$\mathcal{L}_{D}(z_{\gamma}) = \sum_{}^{} \mid f(x) – f(G(z_{\gamma}))\mid$$

識別器の中間層$$f(\cdot)$$の出力は、入力画像の統計量を指定するために参照される。この新しい誤差関数の設計に準拠すれば、zの適応(fitting)は訓練された識別機による困難な決定だけに依存する状況が打破される。生成画像$$G(z_{\gamma})$$が学習された「正常な」画像の分布に適合するか否かは、ここでは何の問題にもならない。重要となるのは、この識別誤差の設計によって、敵対的生成ネットワークは、識別器によって学習された特徴表現の情報を利用して最適化を実行できるようになるということである。

AnoGANの誤差関数は、以上の分析と設計から、トレードオフのハイパーパラメタとなるλを使用して、次のように総括される。

$$\mathcal{L}(z_{\gamma}) = (1 – \lambda) \mathcal{L}_R(z_{\gamma}) + \lambda \mathcal{L}_D(z_{\gamma})$$

異常度の定義

新しいデータに潜む「異常な」データの検知過程では、新しいクエリ画像xを「正常な」画像か「異常な」画像として評価することになる。潜在空間への写像に使用される上記の誤差関数は、全ての更新の反復$$\gamma$$において、敵対的生成ネットワークの訓練中に見出される生成画像$$G(z_{\gamma})$$とクエリ画像の互換性(compatibility)を評価する。そのため、異常度(anomaly score)、すなわち「正常な」画像のモデルに対するクエリ画像xの適合度を表すスコアは、上記の誤差関数から直接的に導くことができる。

$$A(x) = (1 – \lambda) \cdot R(x) + \lambda \cdot D(x)$$

ここで、残差スコアR(x)と識別スコアD(x)はそれぞれ学習済みパラメタを前提に算出された残差誤差と識別誤差を表す。上記の異常度が高ければ、モデルは「異常な」画像を観測したことを意味する。加えて残差スコアは、「正常な」画像と比べてどの画像領域に「異常な」特徴が含まれているのかを指し示している。このスコアは、単に「異常な」画像を抽出するだけではなく、具体的にどの部分が「異常」であると推論できるのかも示してくれているのである。

問題解決策：BiGAN

Zenati, H., et al. (2018)は、Donahue, J., et al.(2016)が提案した「双方向型敵対的生成ネットワーク(Bidirectional Generative Adversarial Networks: BiGANs)」に基づいた異常検知モデルを設計している。単一の潜在的な分布から任意の複合的なデータ分布へと写像するように訓練された生成器のモデルは、直観的(Intuitively)に言えば、潜在意味表現を予測するべく学習しているために、意味論が関連する問題設定においては有用に機能することが経験的に知られている。しかしながら、既存のGANのネットワーク構造は、逆写像、つまりデータを逆に潜在空間へと投射する際には何ら機能しない。Donahue, J., et al.(2016)のBiGANは、この逆写像の学習を可能にしている。BiGANによって学習された特徴表現は、教師あり学習に限らず、教師なし学習や半教師あり学習においても有用となる。

BiGANは識別器と生成器のネットワーク構造に符号化器Eを追加した構成となっている。Eはデータxを潜在表現zに写像する。BiGANにおける識別器Dは、真のデータと生成器Gによって生成されたG(z)を識別するだけではなく、データ空間と潜在空間の組み合わせを識別する。つまり、(x, E(x))と(G(z), z)の識別だ。

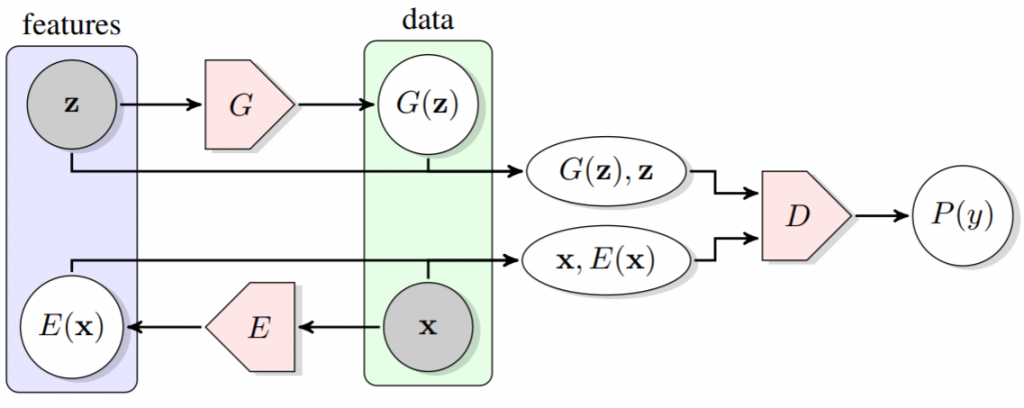
Donahue, J., Krähenbühl, P., & Darrell, T. (2016). Adversarial feature learning. arXiv preprint arXiv:1605.09782., p2.

Eのネットワーク構造はGのそれを反転させた構造となる。EはGの逆写像になる。EとGは直接的に情報を伝播し合う関連を持たない。つまり、EはGの生成データを決して観測せず、GはEの符号化データを決して観測しない。E(G(z))はあり得ず、G(E(x))もあり得ない。しかしながら、EとGは、共通の価値関数を介して、Dを欺くという目的を共有している。価値関数に促されるために、EとGは、相互に相手の逆写像を学習していくことになる。

E、G、Dの価値関数は次のようになる。

$$V(D, E, G) = \mathbb{E}_{x \sim p_X} [\mathbb{E}_{z \sim p_{E(\cdot \mid x)}}[\log D(x, z)]] + \mathbb{E}_{z \sim p_Z}[\mathbb{E}_{x \sim p_{G(\cdot \mid z)}}[1 – \log D(x, z)]]]$$

ここで、$$p_X(x), p_Z(x)$$はそれぞれデータの分布と潜在表現の分布を表す。そして、$$p_E(z \mid x), p_G(x \mid z)$$はそれぞれEとGの分布を表す。

学習済みのBiGANのEは、関連する意味論上のタスクにおいて有用な特徴表現として機能する可能性がある。これは、観測した画像に対して所定の意味論上の「ラベル(label)」を予測するように訓練された教師あり学習の画像認識モデルが、その画像集合についての特徴表現として機能することに等しい。言い換えれば、BiGANのEによって得られるzの推論値は「ラベル」の機能的等価物である。しかしそれはラベル付けやアノテーションを介さずに「無料(free)」で得られる「ラベル」である。

Zenati, H., et al. (2018)は、Donahue, J., et al.(2016)のBiGANを異常検知モデルとして応用する際に、異常度をSchlegl et al. (2017)の設計に従って定義している。ただしBiGANの場合はDの出力にGのみならずEも介在するため、識別誤差は次のようになる。

$$\mathcal{L}_D(x) = \mid \mid f_D(x, E(x)) – f_D (G(E(x)), E(x))\mid\mid$$

問題解決策：GANomaly

Akcay, S., et al. (2018)が提案したGANnomalyのネットワーク構造は、二つの符号化器(Encoder)、一つの復号化器(Decoder)、そして識別器によって構成されている。生成器は、自己符号化器(Auto-Encoder)と第二の符号化器によって構成されている。識別器の構造は、この第二の符号化器の構造に一致している。Akcay, S., et al. (2018)はこのネットワーク構造を前提に三つの誤差関数を設計している。

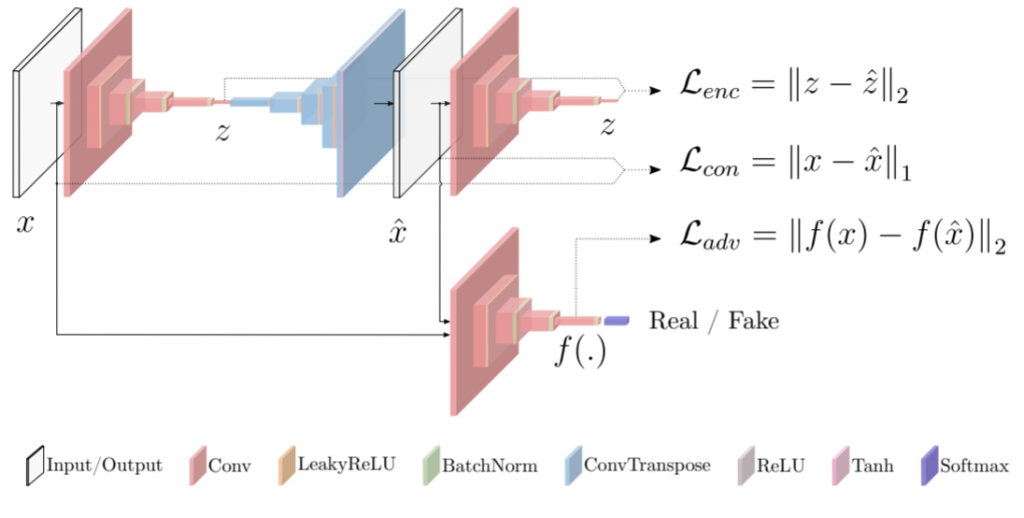
Akcay, S., Atapour-Abarghouei, A., & Breckon, T. P. (2018, December). Ganomaly: Semi-supervised anomaly detection via adversarial training. In Asian Conference on Computer Vision (pp. 622-637). Springer, Cham., p626.

一つ目の誤差関数は「敵対的誤差(Adversarial Loss)」である。Akcay, S., et al. (2018)は、Schlegl et al. (2017)らと同様に、この敵対的誤差$$\mathcal{L}_{adv}$$に特徴照合(feature matching)を利用している。しかしながら、この敵対的誤差だけでは、生成器は入力データに関する文脈情報(contextual information)の学習においては最適化されない。そこでAkcay, S., et al. (2018)は「文脈誤差(Contextual Loss)」の関数$$\mathcal{L}_{con}$$を設定する。この誤差は、入力と生成データの距離を測定することによって算出される。敵対的誤差と文脈誤差により、生成器は文脈上の健全なデータを生成できるようになる。これら二つの誤差関数に加えて、Akcay, S., et al. (2018)は「符号化誤差(Encoder Loss)」の関数$$\mathcal{L}_{enc}$$を設計している。これは生成データと符号化された生成データの距離によって計算される。

GANomalyを前提とした場合、異常度は次のように定義される。

$$\mathcal{A}(\hat{x}) = \mid\mid G_E(\hat{x}) – E(G(\hat{x}))\mid\mid$$

ここで、$$\hat{x}$$はテストデータのサンプルを表す。

派生問題：表現学習の正則化問題

Schlegl et al. (2017)のAnoGANは、GANの潜在ベクトルがデータの真の分布を表現するという仮説から出発することで、潜在ベクトルに基づいて事前学習済みのGANを最適化することにより、潜在ベクトルを再写像する戦略を採っている。しかしその代償として、再写像の計算複合性を引き受けることとなる。Zenati, H., et al. (2018)のBiGANを用いた異常検知モデルは、逆写像の学習を促すネットワーク構造を構成することで、AnoGANが直面した計算複合性を縮減することを可能にしている。一方、Akcay, S., et al. (2018)が提案したGANnomalyは、AnoGANのような二段階の学習過程を踏まずに訓練を済ませることを可能にすることで、モデルの訓練とその後の推論の双方に対して効率的なアルゴリズムを提供している。

GANomalyはMakhzani, A., Shlens, & Goodfellow, I., et al. (2015)によって提唱された敵対的自己符号化器(adversarial autoencoder)に近しい構造を有している。だが生成器として展開されている自己符号化器は、「画像と潜在ベクトル空間の双方で訓練データの分布を捕捉する」(Akcay, S., et al. 2018, p634.)ために、encoder-decoder-encoderのパイプラインとして構造化されている。この観点から観れば、Akcay, S., et al. (2018)の設計観点もまたSchlegl et al. (2017)やZenati, H., et al. (2018)と同じように、潜在ベクトル空間の表現学習に向けられていることがわかる。この表現学習こそが、自己符号化器の特筆すべき機能であるからだ。

思えばGANomalyの生成器として設計されているencoder-decoder-encoderのネットワーク構造は、丁度Zhang, K., Grauman, K., & Sha, F. (2018)がLSTMのEncoder/Decoderを拡張することで設計したRetrospective Encodersの構造に酷似している。

Retrospective EncodersはSeq2Seq(sequence-to-sequence)を構造的に拡張させたRe-Seq2Seqというモデルを採用している。Seq2Seqの符号化器(Encoder)のモデルは、入力されたオリジナルの映像を観察すると共に、観測データ点の意味論的な意味(the semantic meaning)を表現した特徴点を出力する。その後この特徴点は復号化器(Decoder)のモデルによって観察される。ここまでは単なるEncoder/Decoderのモデルと同様の構造となる。一方、Re-Seq2Seqの場合は、この復号化器(Decoder)に更なる別途の符号化器(Encoder)が構造的に結合する。これを特にRetrospective Encoder(Re-Encoder)と呼ぶ。このRe-Encoderの機能は、「要約の意味論的な意味を表現する特徴点(the semantic meaning of the summary)」を推論することである。もしこの要約が重要度の高い情報を保持すると共にオリジナルの映像に関する情報を保持しているのならば、下図のように、初めのEncoderによる特徴表現とRe-Encoderによる特徴表現は、ユークリッド距離をはじめとした一定の距離形式において類似すると期待できる。

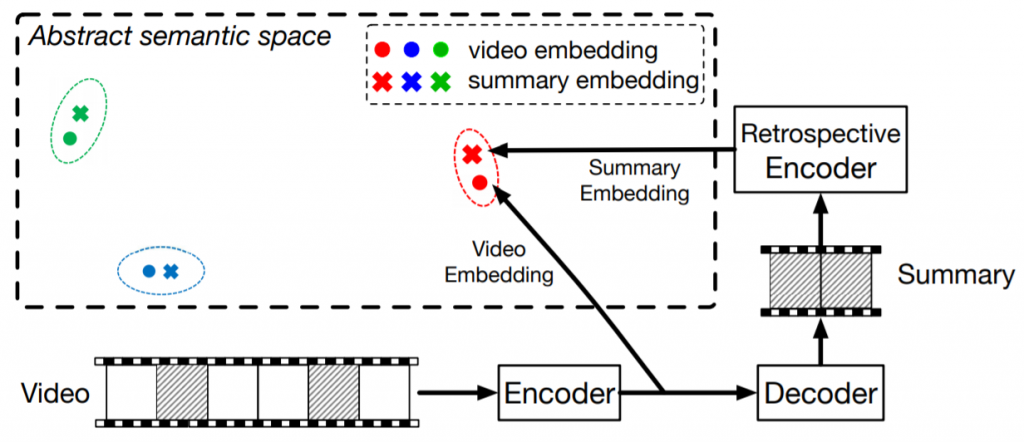
Zhang, K., Grauman, K., & Sha, F. (2018). Retrospective Encoders for Video Summarization. In Proceedings of the European Conference on Computer Vision (ECCV) (pp. 383-399), p2.より掲載。

その誤差関数の設計の背景にある直観(intuition)によれば、EncoderとRe-Encoderの出力は、入力と同一の量の情報を伝達するべきであるとされる。これが要約の目標となる、良き要約とは、要約を閲覧した際に、その閲覧者がオリジナルの映像の全てを閲覧した場合と同一の量の情報を得るような要約である。

この直観は多様体仮説を前提としている。自己符号化器やEncoder/Decoderは、確率的勾配降下法に基づいたミニバッチ単位での学習を反復することによって、その再構成誤差の最小化の過程で、観測データの全体像に対応する確率分布を前提とした表現学習を敢行する。この過程から各モデルは、その隠れ層において、当の確率分布に関する特徴を埋め込むことになる。つまりこの隠れ層に蓄積された情報が、入力された観測データ点の全体の＜代理表象＞を意味するのである。

したがって換言するなら、Re-Encoderによる要約の特徴表現がEncoderによる全体の特徴表現に近接すれば、それだけその要約は良き要約であるということになる。隠れ層に埋め込まれる情報は、各観測データ点に依存する。その埋め込まれた情報の特徴が、当の観測データ点の特徴なのである。故に、Encoderによって埋め込まれた特徴とRe-Encoderによって埋め込まれた特徴を比較すれば、＜全体の特徴＞と＜要約の特徴＞の比較を観測データ点ごとに実施したことになる。初めのEncoderによる特徴表現とRe-Encoderによる特徴表現がユークリッド距離によって比較されるのならば、その距離の大小が、各観測データ点の要約の良質さを物語るという訳だ。

以上の多様体表現の理論に基づく抽象化を前提とすれば、Re-Seq2Seqのモデルは、原理的には自己符号化器や敵対的自己符号化器、そしてEncoder/Decoderに入力し得る観測データ点として前処理できる如何なるデータに関しても適用可能であろう。例えば同じく系列を扱うニューラルネットワーク言語モデルや音声認識などのような問題領域でも再利用することができる。GANomalyのネットワーク構造は、この多様体仮説に準拠した自己符号化器やSeq2Seqの理論を継承した構造になっている。そのため双方のモデルは、潜在ベクトルがデータの真の分布の表現学習問題において、機能的に等価な問題解決策になっている。

したがって、GANomalyは他の表現学習のモデルとの機能的な比較の観点――つまり、何が表現の良し悪しを規定しているのかという問題設定の枠組みの中で、データを生成した潜在的な変動の原因因子、とりわけ参照している問題領域でのアプリケーションに関連する因子を紐解く理想的な表現を追究して設計された他のモデルとの比較の観点――に曝されることになる。表現学習のアルゴリズムの大多数は、この潜在的な変動の因子を学習によって発見するための手掛かりを導入することに基づいている。この手掛かりによって、学習するモデルは観測された因子を他の因子から区別することができるようになる。

豊富なラベルなしサンプルを活用するために、表現学習は潜在的な因子に関する手掛かりを利用する。GANの敵対的なネットワーク構造は、この手掛かりの一種に過ぎない。それは別の手掛かりもあり得るということである。例えば入力空間の近傍を汎化するための「滑らかさ(Smoothness)」なのか、幾つかの因子の間の関連の「線形性」なのか、あるいは複数の潜在的な説明因子の発見こそを重視すべきなのか、説明因子の階層性や深さこそがものを言うのか、自然なクラスタリングや時空間のコヒーレンスが鍵となるのか、特徴量のスパース性を目指した事前分布を設計するべきなのか、いずれにせよこれらの手掛かりは、学習アルゴリズムの設計者が学習するモデルを方向付けるために課した暗黙的な事前信念の形式を取っている。ノーフリーランチ定理は普遍的に妥当する正則化戦略を発見することが不可能であることを指摘している。しかし深層学習の目的の一つは、異常検知問題や分類問題などのように、人間や動物が解決できる問題に類j敷いた様々な問題に適用可能な、「それなりに一般的な」正則化戦略の集合を発見することである。

それ故にGANを用いた異常検知問題も、表現学習の正則化問題として再設定せざるを得ない。それは、たまたま目に付いた「最先端(state-of-the-art)」のGANを教条主義的に崇拝してその結果に一喜一憂するのではなく、実際のアプリケーションでの個別具体的な「正常」と「異常」の意味論を前提とした上で、にも拘わらず諸概念の抽象化に基づいた複数の正則化機能の比較を徹底しなければならないことを意味する。

参考文献

Akcay, S., Atapour-Abarghouei, A., & Breckon, T. P. (2018, December). Ganomaly: Semi-supervised anomaly detection via adversarial training. In Asian Conference on Computer Vision (pp. 622-637). Springer, Cham.
Donahue, J., Krähenbühl, P., & Darrell, T. (2016). Adversarial feature learning. arXiv preprint arXiv:1605.09782.
Makhzani, A., Shlens, J., Jaitly, N., Goodfellow, I., & Frey, B. (2015). Adversarial autoencoders. arXiv preprint arXiv:1511.05644.
Salimans, T., Goodfellow, I., Zaremba, W., Cheung, V., Radford, A., & Chen, X. (2016). Improved techniques for training gans. In Advances in neural information processing systems (pp. 2234-2242).
Schlegl, T., Seeböck, P., Waldstein, S. M., Schmidt-Erfurth, U., & Langs, G. (2017, June). Unsupervised anomaly detection with generative adversarial networks to guide marker discovery. In International conference on information processing in medical imaging (pp. 146-157). Springer, Cham.
Yeh, R., Chen, C., Lim, T. Y., Hasegawa-Johnson, M., & Do, M. N. (2016). Semantic image inpainting with perceptual and contextual losses. arXiv preprint arXiv:1607.07539, 2(3).
Zhang, K., Grauman, K., & Sha, F. (2018). Retrospective Encoders for Video Summarization. In Proceedings of the European Conference on Computer Vision (ECCV) (pp. 383-399).
Zenati, H., Foo, C. S., Lecouat, B., Manek, G., & Chandrasekhar, V. R. (2018). Efficient gan-based anomaly detection. arXiv preprint arXiv:1802.06222.