問題設定:物体検知のドメイン適応問題
「ドメイン適応(domain adaptation)」は転移学習の方法の一種として位置付けられている。ドメイン適応では、タスクと最適な入出力写像は各問題設定で同一であっても、それぞれの入力分布が微妙に異なっているような問題設定での転移学習を指す。ドメイン適応問題の解決策は、「ソースドメイン(source domain)」と「ターゲットドメイン(target domain)」の区別を導入することで探索される傾向にある。この区別は入力されるデータ分布の区別となる。<教師あり学習>の一環として<教師なし学習>を実行する半教師あり学習の形式の場合、「ソースドメイン」は<教師あり学習>の対象となるラベル付きのサンプルの生成分布と見做され、「ターゲットドメイン」は<教師なし学習>の対象となるラベルなしサンプルの生成分布と見做される場合もある。これは、未観測の「ターゲットドメイン」の方が実務上ラベル付きサンプルが得られ難いという実務上の都合を反映している。
ドメイン適応は、ターゲットドメインからラベル付けされていないデータを利用することで、「データセットの偏り(dataset bias)」に対処しようと試みる。実務上、この機能はターゲットデータを手動でラベル付けする作業を減らすことを可能にする。ラベルなしのターゲットデータは、ソースデータのみを利用する場合よりも、アルゴリズムがターゲットドメインでより一般化する上で役立つ補助的な訓練情報を提供する。
それ故、ドメイン適応に成功したアルゴリズムは、データセットの配備の面でも、高い投資対効果を有する。ターゲットドメインから膨大な量のラベル付きサンプルを取得することは、高いコストを要求するか、あるいはそもそも不可能であるためだ。
定式化して観よう。ドメインを$$\mathcal{X} \times \mathcal{Y}$$における確率分布$$\mathcal{D}_{XY}$$と定義する。ここで、$$\mathcal{X}, \mathcal{Y}$$はそれぞれ入力空間と出力空間を表す。ソースドメインとターゲットドメインをそれぞれ$$\mathbb{P}, \mathbb{Q}$$とするなら、ドメイン適応の問題設定から、$$\mathbb{P} \neq \mathbb{Q}$$となる。
これを前提とすれば、教師なしでドメイン適応を実行する場合の目的は、ラベル付きサンプルをソースドメイン$$S^s = \{(x_i^2, y_i^s)\}_{i=1}^{n_s} \sim \mathbb{P}$$から抽出し、ラベルなしサンプルをターゲットドメイン$$S_u^t = \{(x_i^t)\}_{i=1}^{n_t} \sim \mathbb{Q}_X$$から抽出することで、$$S_u^t$$において関数$$f : \mathcal{X} \rightarrow \mathcal{Y}$$の良きラベリングを発見することとなる。教師なしドメイン適応では、特徴の表現学習によって、$$\mathcal{F}$$において$$\mathbb{P}$$と$$\mathbb{Q}$$の分布の差異を最小化するような関数$$g : \mathcal{X} \rightarrow \mathcal{F}$$を発見することが目指される。
ドメイン適応問題は、遅くても2018年ごろには、物体検知問題との関連からも注目されるようになった。多くの物体検知器も、ドメインの変異が生じた場合や、ソースドメインのデータセットバイアスが生じている場合に、性能劣化を伴わせる。それ故近年の物体検知器の多くは、半教師あり学習のアルゴリズムを採用することによって、ソースドメインとターゲットドメインの差異を埋め合わせることを目指して再設計されるようになっている。
問題解決策:ドメイン適応型Faster R-CNN
Chen, Y., et al. (2018)の「ドメイン適応型Faster R-CNN(Domain adaptive faster r-cnn)」は、ドメイン適応問題の枠組みで再設計されたFaster R-CNNの一例となる。ここで想定されるドメインシフト(domain shift)は、主に「共変量シフト(covariate shift)」との関連から記述されている。基本的にこのモデルは、既存のFaster R-CNNを敵対的生成ネットワークのフレームワークに導入する形式で設計されている。
画像水準のドメイン適応とインスタンス水準のドメイン適応の差異
共変量シフトとは、与えられた入力に対する出力の機能的な生成規則は学習時とテスト時で変異せずとも、入力となる共変量の分布が学習時とテスト時で異なる状況を意味する。学習時のデータセットが極端に少ない場合の予測問題は、外挿(extrapolation)あるいは補外に基づく予測となるために、典型的な共変量シフトの状況を派生させる。たとえデータセットに量的な有害性が見当たらずとも、学習用のデータがユーザーによって造り上げられる場合には、当のユーザーのラベル付けやアノテーションに対する注意力次第で、共変量シフトが生じ得る。
共変量シフトの仮定に基づくなら、画像を対象とした物体検知問題におけるドメインシフトとは、「画像水準のドメインシフト(Image-level domain shift)」と「インスタンス水準のドメインシフト(Instance-level domain shift)」に区別できる。画像水準のドメインシフトは、例えば画像のスケール、画像の形状、背景の照明変化などによって派生する可能性がある。一方、インスタンス水準のドメインシフトは、画像で表現されているオブジェクトの外観やサイズによって派生する可能性がある。ドメインの誤差は、この双方の水準で生じていると仮定できる。
ドメインシフトの確率論的な再記述
Chen, Y., et al. (2018)は、共変量シフトの仮定に基づき、ドメインシフトの様相を確率論的に、特にベイズの定理を用いて再記述している。
Chen, Y., et al. (2018)によれば、物体検知問題は、事後分布$$P(C, B \mid I)$$の学習と見做すことができる。ここでIは画像の表現で、Bはオブジェクトのバウンディングボックスを表わす。またCはオブジェクトのカテゴリで、カテゴリ数をKとするなら、$$C \in \{1, …, K\}$$となる。物体検知の学習用のサンプルの結合分布を$$P(C, B, I)$$とし、ソースドメインにおける結合分布とターゲットドメインにおける結合分布をそれぞれ$$P_S(C, B, I), P_T(C, B, I)$$と置く。後者の結合分布は特にドメインシフトの問題を扱う上で参照される。ソースドメインの学習時においては、ターゲットドメインのBとCは未知に留まる。もしドメインシフトが発生しているとするなら、$$P_S (C, B, I) \neq P_T (C, B, I)$$となるはずだ。
ベイズの定理を利用するなら、上記の結合分布は次のように分解できる。
$$P(C, B, I) = P(C, B|I)P(I)$$
分類問題と同じように、物体検知にも共変量シフトが生じ得ると想定するなら、その条件付き分布$$P(C, B \mid I)$$は、ソースドメインとターゲットドメインとで同一となる。そして、ドメインの分布のシフトは、周辺分布$$P(I)$$の差異によってもたらされる。言い換えれば、物体検知器の出力にドメイン間の差異は生じず、一貫していること(consistent)になる。検知結果は、各ドメインからサンプリングされた画像サンプルが何であれ、同様になるはずである。
Faster R-CNNを利用する場合、実際の画像表現Iは畳み込みニューラルネットワークによって出力された特徴写像となる。したがって、ドメインシフトの問題を制御するためには、二つのドメインから得られた画像の表現が同一の分布になるように仕向けなければならない。つまり、$$P_S(I) = P_T(I)$$となる。これが、上述した画像水準のドメイン適応となる。
一方、上述した結合分布は次のようにも分解できる。
$$P(C, B, I) = P(C \mid B, I)P(B, I)$$
共変量シフトの仮定に基づくなら、条件付き分布$$P(C \mid B, I)$$は二つのドメイン間で同一となる。ドメインシフトは、周辺分布$$P(B, I)$$の差異に由来することになる。直観的(Intuitively)に言えば、この同一性は二つのドメイン間の意味論的な一貫性(semantic consistency)を言い表している。オブジェクトが含まれている同一の画像領域が得られたなら、そのカテゴリのラベルもまた、そのドメインに拘わらず、同一となる。したがって、二つのドメインから得られたインスタンス表現の分布は、次のように、同一でなければならない。
$$P_S(B, I) = P_T(B, I))$$
ここで、インスタンス表現(B, I)は、各インスタンスの真のバウンディングボックスにおける画像領域によって抽出された特徴を参照している。そのバウンディングボックスのアノテーションがターゲットドメインでは利用不可能であっても、$$P(B, I) = P(B \mid I)P(I)$$を想定することはできる。ここでいう$$P(B \mid I)$$は、Faster R-CNNに内蔵されているRPNのような、バウンディングボックスの予測モデルとなる。これを前提とすれば、$$P(B \mid I)$$がドメイン不変である場合に限り、以下の解決策が可能になる。
理想的な状況を想定するなら、画像水準とインスタンス水準のいずれかでドメイン同調(domain alignment)が可能になる。
$$P(B, I) = P(B \mid I) P(I)$$と条件付き分布$$P(B \mid I)$$が二つのドメイン間で同一となり、かつ非ゼロとなることを想定するなら、次の関係が得られる。
$$P_S(I) = P_T(I) \Leftrightarrow P_S(B, I) = P_T(B, I)$$
言い換えれば、もし画像水準の表現の分布が二つのドメイン間で同一ならば、インスタンス水準の表現もまた同一となる。そしてこの逆もまた成り立つことになる。しかしながら、条件付き分布$$P(B \mid I)$$を完璧に推定することは、通常単純な課題ではない。理由は二つある。第一に、実用性を重んじるなら、周辺分布$$P(I)$$を完全に揃えるのは困難となるためである。偏りが生じないほどの十分な量を集めることすら難しいかもしれない。第二に、バウンディングボックスのアノテーションはソースドメインの学習データにおいてのみ利用可能となるからである。したがって、$$P(B \mid I)$$はソースドメインのデータにおいてのみ学習できる。
ドメイン不変領域
結局のところ、画像水準とインスタンス水準のドメインシフトは、両立して処理しなくてはならない。この関連からChen, Y., et al. (2018)は、一貫性の正則化を適用することで、$$P(B \mid I)$$を推定する際の偏りを軽減しようとしている。
Chen, Y., et al. (2018)が提案するネットワークは、まずドメイン適応の機能を画像水準における機能とインスタンス水準における機能とに区別した上で、これら二つの機能を担う二つのドメイン適応コンポーネントをそれぞれFaster R-CNNに組み込むことにより構造化されている。各コンポーネントでは、ドメイン分類器を訓練すると共に、敵対的訓練の戦略も採用することで、ドメイン不変(domain-invariant)であるロバストな表現学習機能を実現している。更に、上述した二つの水準に対してそれぞれドメイン分類器を実装することで、これら二つの分類結果に対する一貫性(consistency)に準拠した正則化の戦略も採り入れている。これによりChen, Y., et al. (2018)は、Faster R-CNNにドメイン不変領域を対象とする領域提案ネットワーク(region proposal network: RPN)の学習アルゴリズムを導入している。
H-divergence
H-divergenceは異なる分布からサンプリングされた二つの集合の間のダイバージェンスを測定するために設計されている。特徴ベクトルをxとするなら、ソースドメインからサンプリングされたサンプルとターゲットドメインからサンプリングされたサンプルはそれぞれ$$x_S, x_T$$と表記できる。この二つの集合を識別する機能を担うドメイン分類器$$h : x \rightarrow \{0, 1\}$$は、ソースドメインのサンプルを観測した場合に0を、ターゲットドメインのサンプルを観測した場合に1を、それぞれ出力する。可能なドメイン分類器の集合をHとするなら、H-divergenceは次のように、二つのドメイン間の距離を定義していることになる。
$$\mathcal{d}_{H}(S, T) = 2(1 – \min_{h \in H}({err}_S(h(x)) + {err}_T(h(x))))$$
ここで、$${err}_s, {err}_T$$はそれぞれソースドメインのサンプルとターゲットドメインのサンプルを観測した場合のh(x)の予測誤差を表わす。この定義に準拠した場合、ドメインの距離は、ドメイン分類器hの誤差率に反比例することがわかる。言い換えれば、もしこの誤差率が高ければ、二つのドメインは識別し難いということになる。
特徴ベクトルxを順伝播する深層ニューラルネットワークをfと置く。上述したH-divergenceの関数を前提とすれば、fはドメインの距離が最小化するように特徴ベクトルを出力すれば良いということになる。この観点から我々は、次の関連を導入できる。
$$\min_f \mathcal{d}_{H}(S, T) \Leftrightarrow \max_f \min_{h \in H} \{{err}_S(h(x)) + {err}_T(h(x))\}$$
最適化の観点で見れば、この関連は敵対的となっている。
一貫性の正則化戦略
二つのドメインの分布を同調させるためには、ドメイン分類器に学習を実行させなければならない。物体検知の文脈では、入力xが画像水準の表現Iあるいはインスタンス水準の表現(B, I)となる。上述した確率論的な観点から観れば、h(x)はサンプルxがターゲットドメインに属する確率の推定であると見做せる。
したがって、ドメインのラベルをDとするなら、画像水準のドメイン分類器とインスタンス水準のドメイン分類器はそれぞれ、$$P(D \mid I), P(D \mid B, I)$$と見做せる。ベイズの定理を利用するなら、次の関係が得られる。
$$P(D \mid B, I)P(B \mid I) = P(B \mid D, I)P(D \mid I)$$
とりわけ$$P(B \mid I), P(B \mid D, I)$$はそれぞれドメイン不変のバウンディングボックスの予測器とドメイン依存(domain-dependent)のバウンディングボックスの予測器と見做せる。実用的な観点から観れば、学習させることができるのは、後者の予測器だけである。何故なら、ターゲットドメインのバウンディングボックスのアノテーションは一切入手できないためだ。したがって、二つのドメイン分類器の間の一貫性を$$P(D \mid B, I) = P(D \mid I)$$として強制することで、$$P(B\mid D, I)$$が$$P(B \mid I)$$に近づくように学習することが可能になる。
ドメイン適応型Faster R-CNNの追加誤差関数
以上の設計思想から、ドメイン適応型Faster R-CNNでは、新たに三つの誤差関数が設計されている。その一つが、画像水準のドメイン適応誤差関数である。
画像水準のドメイン適応誤差関数
ソースドメインにおけるi番目の学習用の画像のドメインラベルを$$D_i$$とする。ここで、$$D_I = 1$$の場合、その画像はターゲットドメインの画像となる。更に、畳み込みニューラルネットワークによって出力された特徴写像の(u, v)の位置の活性化関数を$$\phi_{u, v}(I_i)$$とする。ドメイン分類器の出力は$$p_i^{(u, v)}$$となる。すると画像水準のドメイン適応誤差関数は次のようなクロスエントロピー誤差関数となる。
$$\mathcal{L}_{img} = – \sum_{i, u, v}^{}[D_i \log p_i^{(u, v)} + (1 – D_i)\log (1 – p_i^{(u, v)})]$$
各ドメインの分布を調整するためには、ドメイン分類器のパラメタを最適化するために、上記の誤差を最小化していくことになる。上述した敵対的訓練の発想に準じて考えれば、Faster R-CNNのようなベースとなるネットワークを最適化する際には、逆にこのこの誤差は最大化されるように仕向けなければならない。この関連からChen, Y., et al. (2018)は、Ganin, Y., & Lempitsky, V. (2015, June)の「勾配反転層(gradient reversal layer: GRL)」を利用している。
Ganin, Y., & Lempitsky, V. (2015, June)のドメイン適応は、一つの学習過程で、主に特徴の「識別性(discriminativeness)」と「ドメイン不変性(domain-invariance)」を同時に観測することで、ドメイン適応用のネットワークと深層表現学習用のネットワークを接続させることに着目した解決策である。ここで目指されるのは、ドメイン適応を表現学習の過程に組み込むことである。これにより、最終的な分類は、ドメインシフトに対して識別的かつ不変となる。つまりこのドメイン適応に準拠した分類は、たとえターゲットドメインのサンプルを観測した場合であっても、それをソースターゲットと非常に類似した分布へと変換した上で実行される。
尤も、Ganin, Y., & Lempitsky, V. (2015, June)も述べているように、ここで導入されるドメイン適応の大部分は標準的なニューラルネットワークの構造を成している。Ganin, Y., & Lempitsky, V. (2015, June)の提案において固有となるのは、順伝播中には入力を変更せず、しかし逆伝播中には負のスカラー値を乗算することによって勾配を反転させるGRLである。Ganin, Y., & Lempitsky, V. (2015, June)が定式化しているように、GRLの順伝播と逆伝播はそれぞれ次のようになる。
$$R_{\lambda}(x) = x$$
$$\frac{dR_{\lambda}}{dx} = – \lambda I$$
ここで、Iは単位行列を表わす。
インスタンス水準のドメイン適応誤差関数
インスタンス水準の表現は、最終的にはカテゴリの分類器に入力する前のRoIによって得られた特徴ベクトルに準拠している。インスタンス水準の表現を整合させると、オブジェクトの外観、サイズ、画角(viewpoint)などのような局所的なインスタンスの差異を吸収することができるようになる。
画像水準のドメイン適応と同様の手続きを踏むことで、インスタンス水準の分布を整合させるための特徴ベクトルを用いたドメイン分類器の学習も実行できるようになる。i番目の画像におけるj番目の領域提案についてのインスタンス水準のドメイン分類器の出力を$$p_{i, j}$$とするなら、インスタンス水準のドメイン適合誤差関数は次のようになる。
$$\mathcal{L}_{ins} = – \sum_{i, j}^{}[D_i \log p_{i, j} + (1 – D_i) \log (1 – p_{i,j})]$$
尚、このドメイン分類においても、GRLが導入される。
一貫性の正則化
上述した画像水準およびインスタンス水準のドメイン適応誤差関数との関連から言えば、上述した一貫性の正則化戦略は、次のような誤差関数として再記述できる。
$$\mathcal{L}_{cst} = \sum_{i,j}^{}\mid\mid \frac{1}{\mid I \mid}\sum_{u, v}^{}p_i^{(u, v)} – p_{i, j}\mid \mid_2$$
ただしここでのIは画像水準の表現を表す。また$$\mid I \mid$$は活性化された特徴写像の個数の総数を、$$\mid \mid \cdot \mid \mid$$はL2ノルムを表す。
全体の誤差関数
ドメイン適応型Faster R-CNNでは、以上の誤差関数を元々のFaster R-CNNの誤差関数に追加実装することになる。元々の誤差関数を$$\mathcal{L}_{det}$$とするなら、ドメイン適応型Faster R-CNN全体の誤差関数は、次のようになる。
$$\mathcal{L} = \mathcal{L}_{det} + \lambda (\mathcal{L}_{img} + \mathcal{L}_{ins} + \mathcal{L}_{cst})$$
ここで、λはトレードオフパラメタを表す。
機能的等価物:多-敵対的Faster-RCNN
Chen, Y., et al. (2018)のベイズ主義的な視点に触発されたHe, Z., & Zhang, L. (2019)は、同様の問題設定から、ドメイン分布の非一貫性を最小化するために、畳み込み層の各ブロックに複数の敵対的なドメイン分類器を導入することで、階層化されたネットワーク構造によるドメイン適応機能を設計している。
He, Z., & Zhang, L. (2019)が提案する「多-敵対的Faster-RCNN(multi-adversarial FasterRCNN detector: MAF)」では、複数のドメイン分類器のサブモジュールがドメインラベルを識別的に予測するべく学習する。これにより、後続のネットワークはドメイン分類器を混乱させるドメイン不変な特徴を生成するべく学習する。この敵対的なゲームは、end-to-endの学習方法で、GRLに準拠した最適化によって進行する。
多-敵対的Faster-RCNNにおけるGRLは、重み付けの作用が追加された「加重勾配反転層(weighted gradient reversal layer: WGRL)」として拡張されている。WGRLの設計では、ドメイン分類器が観測するサンプルを「混同し易いサンプル(Easily-confused samples)」と「混同し難いサンプル(Hard-confused samples)」に区別される。
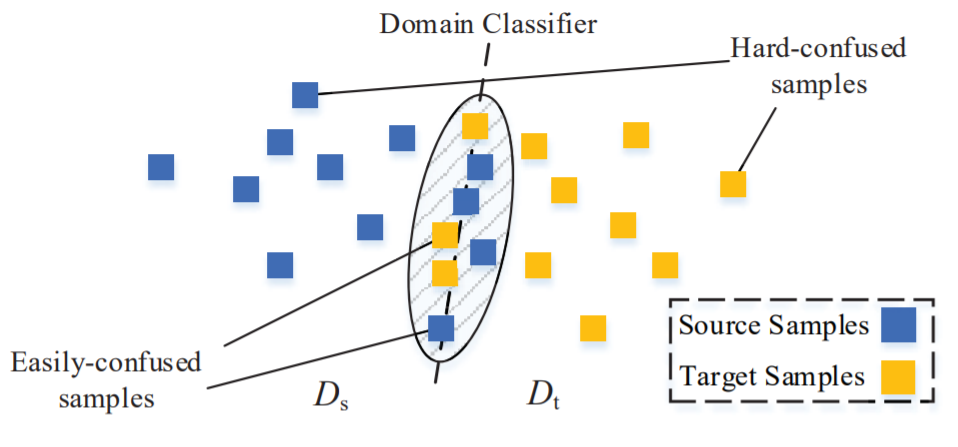
He, Z., & Zhang, L. (2019). Multi-adversarial faster-rcnn for unrestricted object detection. In Proceedings of the IEEE International Conference on Computer Vision (pp. 6668-6677)., p6672.
ソースドメインとターゲットドメインを識別する上では、決定境界に近いサンプルほど、「混同し易いサンプル」となり、識別が困難となる。無論、前者の決定境界から遠い「混同し難いサンプル」の方が識別可能性が高いため、WGRLは、「混同し難いサンプル」を観測した場合に強い正則項を与えることで勾配を逆伝播させれば、ドメインの差異に注意を促せる。
ドメイン分類器の観測したサンプルがソースドメインからサンプリングされている確率をp、ドメインラベルをd、GRLの計算をGとするなら、WGRLは次のように計算される。
$$G_{rev} = – \lambda (d \cdot p + (1 – d)(1 -p))G$$
ここで、λはWGRLのハイパーパラメタを表す。この計算によって予測されたスコアは、勾配の重みとして参照される。ドメイン分類器の確信度が高い場合、ドメイン適応を更に改善していき、サンプルが自動的に加重されることになる。逆にドメイン分類器の確信度が低いサンプルは、識別が付かないサンプルと見做され、重みが小さくなる。
派生問題:第三項排除律
GRLやWGRLを利用した一連のミニマックスゲームは、ドメイン分類器の参照問題がドメインの二値分類であるという前提の上で成り立っている。しかし、設計者が導入するソースドメインとターゲットドメインの区別が第三項排除律を満たさない可能性がある場合は、注意が必要になる。
まさに「混同し易いサンプル」の存在が指し示しているように、ソースドメインとターゲットドメインの区別を導入すれば、排除された第三項がいずれのドメインに属しているのかが気掛かりとなる。ドメインは多値である可能性すらあり得る。第三項排除律が危ぶまれるのは、当の区別とは独立しており、座標系としては直交している別の区別が導入された時である。
問題解決策:ピクセル水準のドメイン適応
一つの問題解消策として挙げられるのは、主に意味論的セグメンテーション(Semantic Segmentation)の問題設定との関連から導入される傾向のある「ピクセル水準のドメイン適応(Pixel-level domain adaptation)」を採用することであろう。このドメイン適応の解決策として導入される個々のモデルは、ターゲットドメインのサンプルをソースドメインのサンプルへと変換する特徴変換器を実装している。こうしたモデルならば、ソースドメインとターゲットドメインの二値分類問題を回避した上で、双方の差異を解消することが可能になると期待できる。
ピクセル水準のドメイン適応については、以下の記事で詳述している。
参考文献
- Chen, Y., Li, W., Sakaridis, C., Dai, D., & Van Gool, L. (2018). Domain adaptive faster r-cnn for object detection in the wild. In Proceedings of the IEEE conference on computer vision and pattern recognition (pp. 3339-3348).
- Ganin, Y., & Lempitsky, V. (2015, June). Unsupervised domain adaptation by backpropagation. In International conference on machine learning (pp. 1180-1189). PMLR.
- He, Z., & Zhang, L. (2019). Multi-adversarial faster-rcnn for unrestricted object detection. In Proceedings of the IEEE International Conference on Computer Vision (pp. 6668-6677).