問題設定:回帰問題と分類問題のマルチタスクとしての物体検知問題
よく話題になっていたように、物体検知器として設計されているFast R-CNN(a Fast Region-based Convolutional Network method)やその拡張系となるFaster R-CNNは、YoLoやSSD(Single Shot MultiBox Detector)と並ぶ物体検知器の代表例として知られている。Fast R-CNNからFaster R-CNNへの「成長」や、YoLoやSSDのような「ライバル」たちとのしのぎを削る競争を表面的に観察するだけであれば、物体検知器の歴史は、日進月歩の研究活動による「右肩上がり」のサクセスストーリーであるかのように思えるかもしれない。
しかし現実としてこの歴史は、決して線的な「進歩(advancement)」の物語ではなかった。むしろその概念史は「進化(evolution)」の歴史として記述せざるを得ない。
実際Fast R-CNNは、元々マルチタスクの誤差関数により、全てのネットワーク層のパラメタを逆伝播で更新していくモデルであった。このモデルは、物体の位置に関する回帰問題と物体のラベルに関する分類問題を同時に解決しようとしている。このモデルの設計で想定される物体検知問題とは、回帰問題と分類問題の複合体を意味している。
だがこうして回帰問題と分類問題の全体として物体検知問題を設定した場合、様々な派生問題を生み出してしまう。単純に表現学習問題の枠組みから観察すれば、分類に特化した表現学習と回帰に特化した表現学習を同時に注力することで、結果的に中途半端な特徴写像しか得られなくなってしまう。それは最終的に性能劣化をもたらす。
画像分類にせよ、映像分類にせよ、行動分類にせよ、画像フレーム内に「小さな物体(small object)」が含まれている場合には、分類性能が著しく低下することもわかっている(Bai, Y., et al., 2018)。更に背景情報が複合的で、特に過密となる場合には、特徴写像の生成部分の性能が低下する(Yang, B., et al., 2018)。こうした派生問題を無視したまま、分類問題と回帰問題の複合体としての物体検知問題に取り組めば、派生問題を予期し切れなくなる。
一方でHe, Z., & Zhang, L. (2019)のように、ドメイン適応問題の問題解決策として展開されるFaster RCNNもある。この観点は特に、ラベル付けやアノテーションの人的コストの派生問題から「教師あり学習」の終焉と「半教師あり学習」の根源が注目されるようになってからは、とりわけ重大な関心事となっている。
一連の関連研究を抽象化して俯瞰するなら、物体検知問題の問題解決策は、様々な派生問題を生み出してきた。こうした事態が計画的な「進歩」によって解決されることは原理的にあり得ない。この事態は「進化」によって解消されている。まさに機械学習の概念史において、チャールズ・ダーウィンの「適者生存(survival of the fittest)」の原理が当て嵌まる訳だ。
様々な問題設定のゲームにおいて「生存」し続け、問題解決策として巧く機能し続けたモデルが、合目的的なモデルとなる。ここでの「選択」の原理となっているのは、概念実証から現実での利用までを含めた実証実験に他ならない。哲学者たちを苛立たせる言い方になるだろうが、これは、「効果」こそが機能の進化の「原因」だということである。こうして機械学習の研究開発の営みは、「サイバネティクス(cybernetics)」となる。サーボ機構に由来する制御の循環システムが、右肩上がりの線形的な進歩史観に取って代わる。
「問題設定」と「問題解決策」の区別の導入から始まる以上の進化論的展望を前提とすれば、物体検知器の概念史を進歩の歴史から区別する観点に立つことで、我々は物体検知器に関する実り多き探索と発見を可能にすると期待できる。この観点に準拠した探索により、少なからず既にコモディティ化され、大衆化されている「ディープラーニング」とは別様の概念として、物体検知器を再記述することが可能になるであろう。以下で再記述していく<問題設定としての物体検知>と<問題解決策としてのFaster R-CNN>の区別は、この進化論的な発見探索のほんの一例に過ぎない。
問題解決策:Fast R-CNN
Fast R-CNNのネットワーク構造が入力として受け取るのは、元画像だけではない。この構造には、「オブジェクト提案(object proposals)」という、オブジェクトが存在する確率の高いと推定された画像内領域の情報も入力される。
Fast R-CNNは、これら二つの情報を入力として受け取り、幾つかの畳み込みとmax pooling層を利用することで、畳み込みの特徴写像を生成する。そして、オブジェクト提案ごとに、RoI Pooling(region of interest pooling)で特徴写像から固定長の特徴ベクトルを抽出する。各特徴ベクトルは、全結合層に伝播され、最終的には二つの出力層に分岐する。その内の一つはオブジェクトの分類機能を担い、もう一つはオブジェクトのバウンディングボックス(bounding-box)の座標値についての回帰の機能を担う。
RoI Pooling
RoI Poolingの機能は、文字通り関心領域(region of interest)の提案である。RoI Poolingは、入力画像のアスペクト比を考慮したMax Poolingを実行する。画像サイズに対応したハイパーパラメタhとwをそれぞれ受け取り、縦幅がHで横幅がWのサイズの画像に対して、は縦幅がh/Hで横幅がw/Wのサイズの窓(window)で分割することで、各サブウィンドウに対応する出力のグリッドセルにMax Poolingが施される。Poolingは、標準的なMax Poolingと同様に、各特徴写像のチャネルごとに適用される。
Fast R-CNNにおけるRoI層は、SPPNets(He, K., et al. 2015)で利用されている「空間ピラミッドプーリング(Spatial Pyramid Pooling: SPP)」を単純化した特殊事例として設計されている。SPPは、畳み込みニューラルネットワークの途中でPooling層を設けることで、入力される画像や特徴写像のサイズの差異を吸収する機能を持つ。RoI層はこのサイズの差分の吸収を前提とした上で、関心領域を固定長のベクトルへと縮減する。
SPPによって得られる特徴写像のスケール不変性は、情報損失を可能な限り無害化しつつ、より小さなサイズの写像を対象とした表現学習を可能にする。従来まで、スケール不変性を獲得するためには、事前に定義されたピクセルサイズで処理する「総当たり(brute force)」的な手法に依存していた。この手法の場合、物体検知器はスケール不変のオブジェクトを訓練データから直接学習しなければならなかった。一方、SPPによって得られる画像ピラミッドは、各オブジェクト提案をほぼそのままスケール正規化することを可能にする。
階層的なサンプリング
Fast R-CNNの学習アルゴリズムは、標準的な画像分類問題とは異なるサンプリングから始まる。その確率的勾配降下法におけるミニバッチは、最初にN個の画像をサンプリングし、次に各画像からR / N個のRoIをサンプリングするという、階層的な手順によって生成される。同一画像に由来するRoIのメモリは、順伝播と逆伝播の双方において共有される。Nを小さくすれば、ミニバッチの計算量も減少する。例えばNが2で、Rが128であれば、Fast R-CNNの学習は128の異なる画像から一つのRoIをサンプリングするよりも約64倍高速化する。
この学習アルゴリズムの場合、サンプリングされる各画像が類似していれば、そのRoIも相関することになる。それ故に訓練の収束が遅延するリスクが指摘される。とはいえGirshick, R. (2015).はこのリスクを実践的(practical)な問題ではないと考えていた。通常のR-CNNよりも少ないエポック数により、N = 2およびR = 128で良好な結果を達成したという。
Fast R-CNNの誤差関数設計
この階層的なサンプリングを前提に、Fast R-CNNは、単純にSoftmaxの分類器の訓練としてではなく、Softmaxの分類問題とバウンディングボックスの回帰問題を同時に最適化しようと学習する。そのためFast R-CNNの出力層は二つに分岐する。一つ目の出力層はRoIごとの離散確率分布で、K+1個のクラスに対して、$$p = (p_0, …, p_K)$$となる。通常、pはK+1次元のSoftmax確率として計算される。二つ目の出力層は、バウンディングボックスの位置情報で、kでインデックス化されたK個のオブジェクトのクラスに対して、$$t^k = (t_x^k, t_y^k, t_w^k, t_h^k)$$となる。この値は、オブジェクト提案に対するスケール不変の変換と、対数空間における高さと幅の関係を指し示す。
それぞれのRoIは、真のラベルuと真のバウンディングボックスvによってラベル付けされる。マルチタスクの誤差関数Lは、このラベル付けされたRoIにおいて計算される。それは以下のように、分類誤差と回帰誤差の複合体として記述される。
$$L(p, u, t^u, v) = L_{cls}(p, u) + \lambda [u \geq 1]L_{loc}(t^u, v) \tag{1}$$
ここで、λはトレードオフの、あるいは二つの誤差の均衡を制御するためのパラメタを表わす。Girshick, R. (2015)は全ての実験で$$\lambda = 1$$を指定している。また$$L_{cls}(p, u) = – \log p_u$$で、真のラベルuにおけるlog-softmax誤差となる。一方、
$$L_{loc}(t^u, v) = \sum_{t \in \{x, y, w, h\}}^{} smooth_{L_1} (t_i^u – u_i) \tag{2}$$
はL1誤差で、L2の誤差を用いた場合よりも外れ値に対してロバストになるように設計されている。回帰問題の目的関数が無制限である場合、L2誤差に伴う訓練では、勾配爆発対策として、学習率を注意深く調節していかなければならなくなる。式(3)は予めこの問題を無害化するために、文字通り平滑化を考慮に入れながら設計されている。
問題解決策:Faster R-CNN
Ren, S., et al. (2015)はFast R-CNNに「領域提案ネットワーク(Region Proposal Networks: RPN)」を導入することで、このモデルを機能的にも構造的にも拡張させたFaster R-CNNを提案した。RPNは、任意のサイズの画像を入力として受け取り、それぞれがオブジェクトであるか否かの判定に用いる「オブジェクト性スコア(objectness score)」を有した長方形のオブジェクト提案の集合を出力する。RPNは畳み込みニューラルネットワークとして構造化されている。このネットワーク構造はFast R-CNNと伝播内容を共有することを前提に設計されている。
RPNのネットワーク構造
RPNは、領域の提案情報を生成するために、最後の畳み込み層によって出力された特徴写像上に小さなネットワークをスライドさせる。このネットワークは、入力された特徴写像のn x nの窓を用いて接続される。nの値はスライディングウインドウのサイズとなる。Ren, S., et al. (2015)では、n=3が採用されている。それぞれのスライディングウインドウは、低次元のベクトルへと写像される。そしてこのベクトルは、オブジェクトの分類を担う層とバウンディングボックスの回帰を担う層へと渡される。
このRPNのネットワークは、n x nの畳み込み層と二つの枝分かれした1 x 1 の畳み込み層として構造化される。このネットワークはスライディングウインドウ方式で動作するため、全結合層では、全ての空間位置情報が相互に共有される。
参照点としてのアンカー
それぞれのスライディングウインドウでは、k個の領域の提案を同時に予測することになる。そのため、回帰を担う層はk個のバウンディングボックスの座標を符号化する4k個の値が出力される。一方、分類を担う層では、それぞれの提案されたオブジェクトがオブジェクトであるか否かの確率を推定する2k個のスコアを出力する。この2k個の提案は、「アンカー(anchors)」と呼ばれるk個の参照ボックスを基準としてパラメタ化される。
それぞれのアンカーは、スライディングウインドウの中心に位置し、スケールとアスペクト比に関連付けられている。それぞれのスライドの位置において、3つのスケールと3つのアスペクト比を利用することで、k = 9のアンカーが生成される。サイズがW x Hの特徴写像を前提とするなら、計WHk個のアンカーが生成される。アンカーとアンカーに関連付けられるオブジェクト提案を計算する関数の双方の観点から観て、このアプローチは「並進不変(translation invariant)」であると見做される。つまり、画像内もしくは特徴写像上のどの位置からであっても、その作用は変わらない。
RPNの学習アルゴリズムでは、各アンカーに二値のラベルが割り当てられる。IoU(Intersection over Union)が最も高いアンカーと真のバウンディングボックスが重なり合う場合や、IoUの重なりが0.7を超えるアンカーと全ての真のバウンディングボックスについては正のラベルを貼る。この場合、真のバウンディングボックスの一つによって、複数のアンカーに正のラベルが付与される場合もあり得る。一方、全ての真のバウンディングボックスにおいて、IoUが0.3未満となる場合には、非正、負のラベルを付与することになる。他方、正でもなければ負でもないアンカーも残存する場合があるが、これらのアンカーは訓練に影響を与えないと想定されている。
RPNの誤差関数
RPNの学習アルゴリズムを前提とした場合でも、誤差関数は分類誤差関数と回帰誤差関数の複合体であるという点では機能的に等価となる。ただし、各関数への入力には微妙な差異がある。
$$L(\{p_i\}, \{t_i\}) = \frac{1}{N_{cls}}\sum_i^{}L_{cls}(p_i, p_i^{\ast}) + \lambda \frac{1}{N_{reg}}\sum_{i}^{}p_i^{\ast}L_{reg}(t_i, t_i^{\ast}) \tag{1}$$
ここで、$$p_i^{\ast}$$はアンカーの真のラベルを表わす。正ならば1となり、負ならば0となる。また$$t_i^{\ast}$$は正のアンカーに関連付けられた真のボックスを表わす。回帰誤差は$$L_{reg}(t_i, t_i^{\ast}) = R(t_i – t_i^{\ast})$$で、$$R = smooth_{L_1}(x)$$となり、Fast R-CNNを踏襲している。回帰誤差の項となる$$p_i^{\ast}L_{reg}$$が言い表すのは、回帰誤差が正のアンカーの場合にのみ逆伝播されるということに他ならない。
上記の回帰誤差関数は、アンカーボックスから近接する真のボックスへのバウンディングボックス回帰誤差関数として想定することができる。アンカーの導入を前提とすれば、各座標値は次のようになる。
$$t_x = \frac{(x – x_a)}{w_a}, \ t_y = \frac{(y – y_a)}{h_a},$$
$$t_w = \log \left(\frac{w}{w_a}\right), \ t_h = \log \left(\frac{h}{h_a} \right),$$
$$t_x^{\ast} = \frac{(x^{\ast} – x_a)}{w_a}, \ t_y^{\ast} = \frac{(y^{\ast} – y_a)}{h_a},$$
$$t_w^{\ast} = \log \left(\frac{w^{\ast}}{w_a} \right), \ t_h^{\ast} = \log \left(\frac{h^{\ast}}{h_a} \right)$$
ここで、xとyはそれぞれ、ボックスの中心点のx座標とy座標を表す。またwとhは、ボックスの横幅と縦幅を表わす。変数$$v, v_a, v^{\ast}$$はそれぞれv(=x, y, w, h)について予測されたボックス、vのアンカーボックス、そしてvの真のボックスを表わす。
この誤差関数は、He, K., et al. (2015)やGirshick, R. (2015)の誤差関数とは異なる関数として設計されている。He, K., et al. (2015)やGirshick, R. (2015)では、任意のサイズの領域からプーリングされた特徴に対してバウンディングボックス回帰が実行される。そして回帰の重みは、全ての領域サイズで共有される。一方でRen, S., et al. (2015)の誤差関数設計では、回帰に利用される特徴が、特徴写像上で同一の空間サイズ、つまりn x nとなる。様々なサイズの特徴を処理するために、ここではk個のバウンディングボックス回帰の集合が学習される。各回帰モデルは、一つのスケールと一つのアスペクト比を担う。そしてこれらの回帰モデルは、互いに重みを共有しない。そのため、特徴のサイズとスケールが固定されている場合であっても、様々なサイズのバウンディングボックスを予測することが可能になる。
畳み込みニューラルネットワークとして実装されたRPNは、逆伝播と確率的勾配降下法によって訓練させることができる。Ren, S., et al. (2015)のサンプリング戦略は、Fast R-CNNのそれを踏襲している。各ミニバッチは、多くの正のアンカーと負のアンカーを含めた単一の画像によって構築される。これにより、全てのアンカーについての誤差関数の最小化が可能になる。だがこのサンプリング戦略では、負のアンカーのサンプルが優勢であるために、負の方向へのデータセットバイアスが派生してしまう。
そこでRen, S., et al. (2015)は、ミニバッチの誤差を計算するために、別の戦略を採用している。サンプリングされた正と負のアンカーの割合が1:1になるように、一個の画像から一様に256個のアンカーをサンプリングしているのである。もし、一個の画像の中に128個未満しか正のサンプルが含まれていない場合、負のサンプルをパディングすることで埋め合わせている。
RPNのFast R-CNNの交互学習
Faster R-CNNのネットワークは、上述したRPNをFast R-CNNに接続させることで構造化されている。この接続を実現するためには、RPNとFast R-CNNの間で共有される畳み込み層のパラメタを共有できるように、学習アルゴリズムを設計しなければならない。
しかしながらこれは、単にRPNとFast R-CNNの双方を含む単一のネットワーク構造を設計し、それを逆伝播によって最適化していけば良いという話でもない。何故なら、Fast R-CNNの訓練は固定長のオブジェクト提案に依存しているためである。オブジェクト提案の機構を動的に変更しながらFast R-CNNを学習した場合、果たして収束するか否かが事前に不明確となる。
それ故Ren, S., et al. (2015)は、RPNとFast R-CNNの同時的な最適化に対して言わば禁欲的な姿勢を貫き、その代わりとして、交互最適化(alternating optimization)の戦略を採用している。この最適化のアルゴリズムは次の4つの手順を踏む。
- RPNの学習。このネットワークは、ImageNetで事前学習したモデルのパラメタで初期化され、領域提案タスク用に、end-to-endで微調整される。
- RPNによって生成された提案を用いたFast R-CNNの学習。これは物体検知器としての学習となる。このネットワークもまたImageNetで事前学習されたパラメタによって初期化される。尚、このステップの時点では、まだ双方のモデルはパラメタを共有してない。
- 物体検知器を利用したRPNの学習。共有される畳み込み層を修正し、RPNに固有の層のみを微調整していく。
- Fast R-CNNの全結合層の微調整。この微調整は、共有された畳み込み層を固定にしたまま実行していく。そのため、双方のネットワークが同一の畳み込み層を共有し、最終的には統合されたネットワークを形成する。
派生問題:Faster R-CNNの性能劣化、その3つの条件
2015年に提唱されて以来、Faster R-CNNはYoLoやSSD(Single Shot MultiBox Detector)と並ぶ物体検知器の代表例として知られることとなった。速度の面ではYoLoに劣るものの、一般的にFaster R-CNNはこの二つのモデルに比して高い精度を発揮していた。
しかしその反面、Faster R-CNNの性能劣化を招く要因についても、知見が深まっている。大別すれば、この要因は三つに区別される(Cheng, B., et al. 2018)。
第一に、たとえ物体の分類は正当できていても、バウンディングボックス上の物体が他の物体と重なり合う場合には、IoU(Intersection over Union)が著しく低下してしまう。この点では、Faster R-CNNはYoLoと共通の弱点を有したままであった。
一方で第二の要因として、逆にバウンディングボックスの精度は高くても、分類で誤る場合もあった。これはとりわけ一部のラベルが同様の識別部分を共有していたために、予測されたバウンディングボックスが真のオブジェクトの情報と上手く整合せず、混雑した識別部分のみにモデルが反応してしまうためであると考えられている。また別の理由としては、物体検知器に内臓されている分類器が、二つの類似したラベルを識別する上で十分な強度に達していないことも挙げられる。
最後に、第三の要因となるのは、「背景(background)」の問題だ。背景から得られる情報が大量にある場合や背景が過密である場合には、畳み込みニューラルネットワークはその多くの情報を観測することで、結果的に不要な情報にまで振り回されてしまうことになる。
問題解決策:分類問題と回帰問題の区別
上述した第一の性能劣化要因を解決するために、Cheng, B., et al. (2018)は分類モデルと回帰モデルにおける特徴の共有部分にメスを入れている。物体検知器は通常、画像の分類モデルからfittingされ、大規模な画像分類データセットを用いて事前学習される。Ren, S., et al. (2015)の場合はImageNetが採用されていた。
こうしたネットワーク構造は、分類問題の解決策として、スケール不変の特徴を学習するべく設計されている。RPNで導入されるアンカーは、参照点として機能することで、並進不変性を成り立たせている。しかし、並進不変性を必要としているのは、分類機能においてであって、回帰機能においてではない。バウンディングボックス回帰において必要となるのは、むしろ「並進共変(translation covariant)」の機能の方である。
つまりFaster R-CNNは、一方では分類モデルとして並進不変性を探索していながら、他方では逆に並進共変性を探索していたことになる。Faster R-CNNの物体検知機能は、分類機能に特化すれば回帰機能が、回帰機能に特化すれば分類機能が、それぞれ損なわれることになる。それ故ImageNetの事前学習から始まるRen, S., et al. (2015)の交互学習は、パラドックス化されたアルゴリズムとなってしまう。このアルゴリズムは、分類機能への特化と回帰機能への特化を交互に反復するだけで、最終的にいずれの機能にも特化できなくなる。
しかしこのパラドックスは、物体検知問題を、分類問題と回帰問題の「全体」として記述した場合に発見される問題に過ぎない。問題は、「全体」を観察しているからこそ、解決不可能になる。「全体」の問題は、一時に解決するのではなく、細分化して解消していくしかない。つまり、分類問題と回帰問題の複合体として記述されてきた物体検知問題を、再び分類問題と回帰問題に区別せざるを得ないのだ。Cheng, B., et al. (2018)が指摘する「特徴共有に基づく問題(Problem with Feature Sharing)」は、既にこの問題設定の混在によって招かれていたと考えて良い。
分類誤差と回帰誤差の差異
この問題の区別は、マルチタスク化された誤差関数の区別に対応付けられる。物体検知問題の誤差関数は、次のように、分類誤差と回帰誤差の和として設計されていた。
$$L_{detection} = L_{cls} + L_{bbox}$$
しかし、「特徴共有に基づく問題」が特徴の疎結合であって、それが分類モデルと回帰モデルの疎結合を意味する以上、誤差関数に対してもまた区別を導入しなくてはならない。さもなければ、Cheng, B., et al. (2018)が指摘するように、物体検知器は全体として二つの誤差の総和を考慮する代償として、二つのタスクの妥協点となる準最適に収束する可能性がある。そこでCheng, B., et al. (2018)は、この二つの誤差の総和を誤差として記述する代わりに、次のように、誤差関数を2種類の誤差関数の結合として設計することで、2段階の学習アルゴリズムを考案している。
$$L_{detection} = [L_{cls} + L_{bbox}, L_{cls}]$$
問題解決策:Decoupled Classification Refinement(DCR)
R-CNNの最も重要な利点は、その受容野が常にROIの全体を捕捉することにある。受容野のサイズは、それぞれのオブジェクト提案を固定サイズにトリミングすることで変更される。これにより、受容野のサイズは、オブジェクトのサイズに応じて調節されている。しかしこの大きな受容野は、文脈情報が正確ではない場合に、逆機能となってしまう。
Ren, S., et al. (2015)も述べていたように、RPNのスライディングウインドウのnに小さな値が代入されれば、入力画像の有効受容野は大きくなる。しかしこの場合、固定の受容野によって導入された文脈の情報量が異なれば、オブジェクトのサイズごとに性能が変わってしまう可能性がある。それ故にCheng, B., et al. (2018)は、大きな受容野ではなく適応的な受容野(adaptive receptive field)を優先すべきであると主張する。つまり、物体検知器の構造がオブジェクトのサイズに応じて可変となるようなネットワークが必要となるのである。
各オブジェクトに伴う文脈情報はそのサイズに比例する必要がある。しかし、文脈情報の量を決定する方法は未解決問題であった。それでも適応的な受容野によって得られる特徴写像は、オブジェクトにより良く整合しているという。適応的な受容野を利用すれば、物体検知器は常にオブジェクト全体に注意を向け、予測を実行するために整合された特徴変換を可能にする。
この関連からCheng, B., et al. (2018)は、Faster R-CNNの物体検知器全体としての性能を向上させるために、Decoupled Classification Refinement (DCR)という新しいモジュールを提案している。
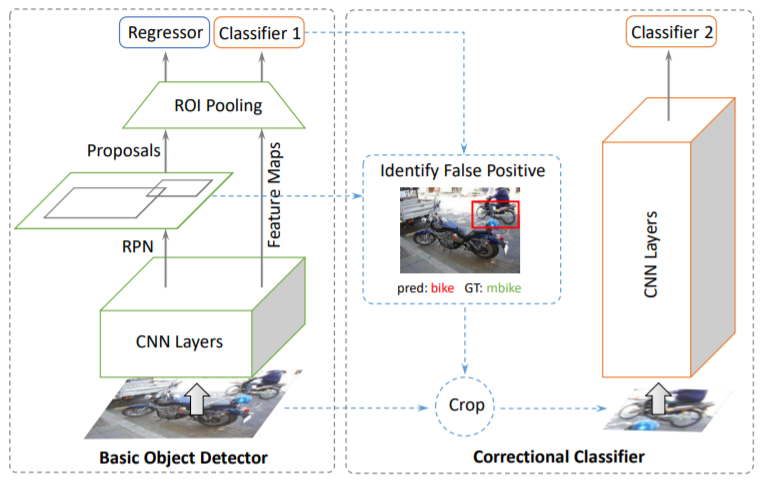
Cheng, B., Wei, Y., Shi, H., Feris, R., Xiong, J., & Huang, T. (2018). Revisiting rcnn: On awakening the classification power of faster rcnn. In Proceedings of the European conference on computer vision (ECCV) (pp. 453-468)., p460.
DCRモジュールは、分類問題における並進不変性の品質を維持するために、特徴の共有を破棄している。更に、DCRモジュールとFaster R-CNNの間では誤差も伝播しない。そのため、一方の誤差の最小化が他方の誤差の最小化に逆機能をもたらすことも無い。このネットワーク構造の分離によって、バウンディングボックス回帰問題のための位置情報に注意を向ける物体検知器側と、分類問題に注力するDCRモジュールの機能的な分化が成立する。
DCRモジュールはバウンディングボックスのサイズを事前に定義されたサイズに変更することで、適応受容野を導入している。DCRの出力の特徴写像だけを観察するならROI Poolingと機能的に等価だが、ROI Poolingは豊富な文脈情報を保持するため、より大きな領域を検知してしまう。Small Object Detectionやobject外の背景情報が複合的となる場合は特に、DCRが推奨される。
参考文献
- Bai, Y., Zhang, Y., Ding, M., & Ghanem, B. (2018). Sod-mtgan: Small object detection via multi-task generative adversarial network. In Proceedings of the European Conference on Computer Vision (ECCV) (pp. 206-221).
- Cheng, B., Wei, Y., Shi, H., Feris, R., Xiong, J., & Huang, T. (2018). Revisiting rcnn: On awakening the classification power of faster rcnn. In Proceedings of the European conference on computer vision (ECCV) (pp. 453-468).
- Girshick, R. (2015). Fast r-cnn. In Proceedings of the IEEE international conference on computer vision (pp. 1440-1448).
- He, K., Zhang, X., Ren, S., & Sun, J. (2015). Spatial pyramid pooling in deep convolutional networks for visual recognition. IEEE transactions on pattern analysis and machine intelligence, 37(9), 1904-19
- He, Z., & Zhang, L. (2019). Multi-adversarial faster-rcnn for unrestricted object detection. In Proceedings of the IEEE International Conference on Computer Vision (pp. 6668-6677).
- Ren, S., He, K., Girshick, R., & Sun, J. (2015). Faster r-cnn: Towards real-time object detection with region proposal networks. In Advances in neural information processing systems (pp. 91-99).
- Yang, B., Cao, J., Ni, R., & Zou, L. (2018). Anomaly Detection in Moving Crowds through Spatiotemporal Autoencoding and Additional Attention. Advances in Multimedia, 2018.