問題設定:ドメイン適応問題
「ドメイン適応(domain adaptation)」は転移学習の方法の一種として位置付けられている。ドメイン適応では、タスクと最適な入出力写像は各問題設定で同一であっても、それぞれの入力分布が微妙に異なっているような問題設定での転移学習を指す。
最も早期の先行事例の一つは「感情分析(Sentiment analysis)」の文脈で応用された。感情分析の問題設定では、ネット通販のクチコミなどの自然文の内容に対して、ポジティブな感情から記述されたコメントとネガティブな感情から記述されたコメントの識別を試みる。
ドメイン適応は、書籍、ビデオ、音楽などのメディアにおけるレビュー内容で学習した感情予測器を、後からテレビやスマートフォンなどのような家電製品に関するコメントの分析にも再利用する際にも機能する。この場合、全ての記述をポジティブ、ニュートラル、ネガティブのいずれかに割り当てる潜在的な関数を想定することができる。だが無論、あるドメインと他のドメインとでは、語彙や文体が異なっている。複数のドメインでそれらを一般化するのは困難となる。
問題解決策:ソースドメインとターゲットドメインの区別
ドメイン適応問題で導入される主な区別は、「ソースドメイン(source domain)」と「ターゲットドメイン(target domain)」の区別である。この区別は入力されるデータ分布の区別となる。<教師あり学習>の一環として<教師なし学習>を実行する半教師あり学習の形式の場合、「ソースドメイン」は<教師あり学習>の対象となるラベル付きのサンプルの生成分布と見做され、「ターゲットドメイン」は<教師なし学習>の対象となるラベルなしサンプルの生成分布と見做される場合もある。これは、未観測の「ターゲットドメイン」の方が実務上ラベル付きサンプルが得られ難いという実務上の都合を反映している。
ドメイン適応は、ターゲットドメインからラベル付けされていないデータを利用することで、「データセットの偏り(dataset bias)」に対処しようと試みる。実務上、この機能はターゲットデータを手動でラベル付けする作業を減らすことを可能にする。ラベルなしのターゲットデータは、ソースデータのみを利用する場合よりも、アルゴリズムがターゲットドメインでより一般化する上で役立つ補助的な訓練情報を提供する。
それ故、ドメイン適応に成功したアルゴリズムは、データセットの配備の面でも、高い投資対効果を有する。ターゲットドメインから膨大な量のラベル付きサンプルを取得することは、高いコストを要求するか、あるいはそもそも不可能であるためだ。
定式化して観よう。ドメインを$$\mathcal{X} \times \mathcal{Y}$$における確率分布$$\mathcal{D}_{XY}$$と定義する。ここで、$$\mathcal{X}, \mathcal{Y}$$はそれぞれ入力空間と出力空間を表す。ソースドメインとターゲットドメインをそれぞれ$$\mathbb{P}, \mathbb{Q}$$とするなら、ドメイン適応の問題設定から、$$\mathbb{P} \neq \mathbb{Q}$$となる。
これを前提とすれば、教師なしでドメイン適応を実行する場合の目的は、ラベル付きサンプルをソースドメイン$$S^s = \{(x_i^2, y_i^s)\}_{i=1}^{n_s} \sim \mathbb{P}$$から抽出し、ラベルなしサンプルをターゲットドメイン$$S_u^t = \{(x_i^t)\}_{i=1}^{n_t} \sim \mathbb{Q}_X$$から抽出することで、$$S_u^t$$において関数$$f : \mathcal{X} \rightarrow \mathcal{Y}$$の良きラベリングを発見することとなる。教師なしドメイン適応では、特徴の表現学習によって、$$\mathcal{F}$$において$$\mathbb{P}$$と$$\mathbb{Q}$$の分布の差異を最小化するような関数$$g : \mathcal{X} \rightarrow \mathcal{F}$$を発見することが目指される。
問題解決策:深層再構成分類ネットワーク
理想的には、識別的な表現はラベルとデータ構造の双方をモデル化するべきである。直観(intuition)に基づいて言えば、ドメイン適応表現は次の二つの評価水準を満たすべきである。第一の評価基準は、ラベル付けされているソースドメインのデータを分類することに関わる。故に分類問題としての評価水準が満たされなければならない。第二の評価基準は、ラベルなしのターゲットドメインを再構成する場合の評価基準である。これは識別的な表現の近似と見做すことができる。
この関連で言えば、「深層再構成分類ネットワーク(Deep Reconstruction-Classification Network: DRCN)」は、半教師あり学習を応用したドメイン適応のモデルの一例となる。このモデルは特に「教師ありドメイン適応(supervised domain adaptation)」と「教師なしドメイン適応(unsupervised domain adaptation)」の区別を導入することで、<教師なし学習>とドメイン適応の接点を明確化する理論を提供してもいる。
深層再構成分類ネットワークのモデルには、符号化された表現を共有する二つのパイプラインが実装されている。第一のパイプラインでは、通常の深層畳み込みニューラルネットワークによるソースドメインのラベルの予測を実行する。第二のパイプラインは、ターゲットドメインのデータを再構成するための畳み込み自己符号化器として機能する。
したがって、深層再構成分類ネットワークはマルチタスク学習(multitask learning)を通じて最適化される。つまり、半教師あり学習のように、教師あり学習と教師なし学習を接続させることで最適化される。符号化された表現を共有する狙いは、ドメインを跨いで有用となる情報を提供するこれらマルチタスクにおける共通性を学習することである。
深層再構成分類ネットワークの構造
より定式化して言えば、深層再構成分類ネットワークは、次のように再記述できる。教師あり学習のラベル予測用のパイプラインを$$f_c : \mathcal{X} \rightarrow \mathcal{Y}$$とし、教師なし学習による再構成用のパイプラインを$$f_r : \mathcal{X} \rightarrow \mathcal{Y}$$とする。更に、上述した符号化と復号化の表現学習を次のように定義しよう。
$$g_{enc} : \mathcal{X} \rightarrow \mathcal{F}$$
$$g_{dec} : \mathcal{F} \rightarrow \mathcal{X}$$
特徴表現に対するラベル付けは次のようになる。
$$g_{lab} : \mathcal{F} \rightarrow \mathcal{Y}$$
m個の多クラス分類問題として観察するなら、$$g_{lab}$$の出力値はソフトマックス関数の出力値となる。入力を$$x \in \mathcal{X}$$とするなら、次のように分解することができる。
$$f_c(x) = (g_{lab} \circ g_{enc})(x)$$
$$f_r(x) = (g_{dec} \circ g_{enc})(x)$$
教師あり学習のモデルと教師なし学習のモデルにおけるパラメタをそれぞれ$$\theta_c = \{\theta_{enc}, \theta_{lab}\}$$と$$\theta_r = \{\theta_{enc}, \theta_{dec}\}$$とする。$$\theta_{enc}$$は$$g_{enc}$$の特徴写像のために共有されるパラメタである。$$\theta_{enc}, \theta_{dec}, \theta_{lab}$$は複数の層においてパラメタを符号化するであろう。ここで重要となるのは、特徴写像$$g_{enc}$$が$$f_c, f_r$$の双方を支持するようにモデル化することである。
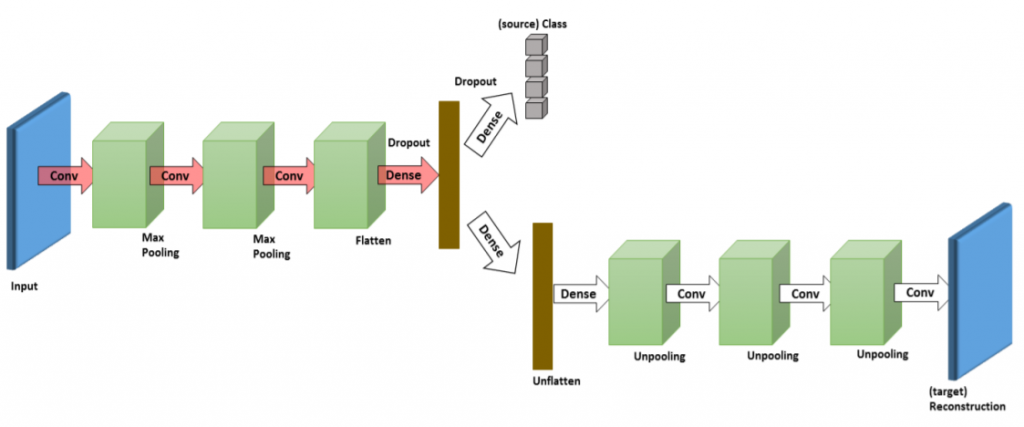
Ghifary, M., Kleijn, W. B., Zhang, M., Balduzzi, D., & Li, W. (2016, October). Deep reconstruction-classification networks for unsupervised domain adaptation. In European Conference on Computer Vision (pp. 597-613). Springer, Cham., p5.より掲載。
深層再構成分類ネットワークの学習アルゴリズム
学習アルゴリズムは次のように表される。入力を$$\mathcal{X} \subseteq \mathbb{R}^d$$、ラベルを$$\mathcal{Y} \subseteq \mathbb{R}^m$$とする。分類誤差と再構成誤差をそれぞれ$$l_c : \mathcal{Y} \times \mathcal{Y} \rightarrow \mathbb{R}$$と$$l_r : \mathcal{X} \times \mathcal{X} \rightarrow \mathbb{R}$$とする。ソースドメインのサンプルを$$S^s = \{(x_i^s, y_i^s)\}_{i=1}^{n_s} \sim \mathbb{P}$$とし、ラベルのone-hotなベクトルを$$y_i \in {0, 1}^m$$とする。ラベルなしのターゲットドメインのサンプルは$$S_u^t = \{(x_j^t)\}_{j=1}^{n_t} \sim \mathbb{Q}$$となる。
以上を踏まえれば、分類誤差と再構成誤差はそれぞれ次のように再記述できる。
$$\mathcal{L}_c^{n_s}(\{\theta_{enc}, \theta_{lab}\}) := \sum_{i=1}^{n_s}l_c(f_c(x_i^s; \{\theta_{enc}, \theta_{lab}\}), y_i^s)$$
$$\mathcal{L}_r^{n_t}(\{\theta_{enc}, \theta_{dec}\}) := \sum_{j=1}^{n_t}l_r(f_r(x_j^t; \{\theta_{enc}, \theta_{dec}\}), x_j^t)$$
出力がソフトマックス関数であることから、典型的には、$$l_c$$はクロスエントロピーの誤差となる。
$$l_c = \sum_{k=1}^m y_k \log [f_c(x)]_k$$
分類誤差と再構成誤差をトレードオフのパラメタλで統合するなら、目的関数は次のような教師あり学習と教師なし学習の誤差関数として整理できる。
$$\min \lambda \mathcal{L}_c^{n_s}(\{\theta_{enc}, \theta_{lab}\}) + (1 – \lambda)\mathcal{L}_r^{n_t}(\{\theta_{enc}, \theta_{dec}\}), \ 0 \leq \lambda \leq 1$$
学習アルゴリズム全体として観ると、深層再構成分類ネットワークは、分類誤差最小化に基づいたパラメタ更新と再構成誤差最小化に基づいたパラメタ更新をエポックごとに交互に実行している。したがって実際には、$$\theta_c$$と$$\theta_r$$が更新されるタイミングには差異がある。
この誤差関数は確率的勾配降下法をはじめとしたアルゴリズムで最適化される。正則化の技術としては、ドロップアウトのような一般的な方法が採用される。またこれも正則化の狙いがあってのことであるが、自己符号化器の構造はノイズ除去型自己符号化器の様相を呈している。最適化されたパラメタ$$\hat{\theta}_{enc}, \hat{\theta}_{lab}$$はそれぞれ分類モデル$$f_c(x^t; \{\hat{\theta}_{enc}, \hat{\theta}_{lab}\})$$として再利用される。この分類モデルは、ターゲットドメインにおいても機能すると期待される。
最尤推定の近似
上述した通り、深層再構成分類ネットワークの目的関数は教師あり学習における誤差関数と教師なし学習における誤差関数の複合体である。この意味でこの目的関数は、ターゲットドメインにおける半教師あり学習として機能する。このような目的関数設計において想定されているのは、教師なし学習それ自体は、ラベルなしのデータでも十分であるということだ。このことは、教師なしのソースデータを追加してもドメイン適応が改善される訳ではないということを予期させる。
ラベル付きデータとラベルなしデータをそれぞれ$$\mathbb{D}_{XY} =: \mathbb{D}$$と$$\mathbb{D}_X$$とする。最尤推定で学習する、$$\theta \in \Theta$$でパラメタ化されているモデルの族を$$P^{\theta}(\cdot)$$とする。ドメイン適応問題における深層再構成分類ネットワークのアルゴリズムで確率論的に想定されているのは、$$P^{\theta}(x)$$がガウス分布に従うと共に$$P^{\theta}(y\mid x)$$がロジスティクス回帰に適合した多項分布に従うということである。したがって、上記の目的関数は次の最尤推定と等価となる。
$$\newcommand{\argmax}{\mathop{\rm arg~max}\limits}$$$$\hat{\theta} = \argmax_{\theta} \lambda \sum_{i=1}^{n_s} \log P_{Y \mid X}^{\theta}(y_i^s \mid x_i^s) + (1 – \lambda)\sum_{j=1}^{n_t} \log P_{X \mid \tilde{X}}^{\theta}(x_j^t \mid \tilde{x}_j^t) \tag{1}$$
ここで、$$\tilde{x}$$は$$\mathbb{Q}_{\tilde{X} \mid X}$$によって生成されたノイズ化された入力である。上式の第一項は教師あり学習によって学習したモデルを表現している。第二項は教師なし学習によって学習した自己符号化器のモデルを表す。識別モデルはソースデータの分布$$\mathbb{P}_X$$から抽出されたラベル付きデータのみを観測する。
ターゲットドメイン$$\mathbb{Q}$$からラベル付きサンプルとラベルなしサンプルが確率$$\lambda$$と確率 $$1 – \lambda$$ によって得られるとすると、最尤推定ζは次のようになる。
$$\zeta = \argmax_{\zeta} \lambda \mathbb{E}_Q [\log P^{\zeta}(x, y)] + (1 – \lambda) \mathbb{E}_{\mathbb{Q}_X}[\log P_X^{\zeta}(x)] \tag{2}$$
この定理は、モデルが真の分布を包含しているという「整合性(consistency)」と「円滑性(smoothness)」、そして「測定可能性(measurability)」が成立している場合に満たされる。ターゲットデータ$$(x_1^t, y_1^t), …, (x_{n_t}^t, y_{n_t}^t)$$を受け取る場合、ζは次のように推定される。
$$\hat{\zeta} = \argmax_{\zeta}\lambda \sum_{i=1}^{n_t}[ \log P^{\zeta}(x_i^t, y_i^t)] + (1 – \lambda) \sum_{i=1}^{n_t}[\log P_X^{\zeta}(x_i^t)] \tag{3}$$
しかし、ターゲットドメインのデータを参照することができない以上は、教師なしドメイン適応においてこの最尤推定値を計算することは不可能である。したがって観点を変える必要がある。
$$\hat{\theta}$$と$$\hat{\zeta}$$は密接に関連しているというのは確実である。共変量シフト(covariate shift)によって$$\mathbb{P} \neq \mathbb{Q}$$かつ$$\mathbb{P}_{Y \mid X} = \mathbb{Q}_{Y \mid X}$$を想定するなら、(1)はターゲットサンプルからソースサンプルへの期待値へと変換できる。
$$\mathbb{E}_{\mathbb{Q}}[\log P^{\zeta}(x, y)] = \mathbb{E}_{\mathbb{P}}[\frac{\mathbb{Q}_X(x)}{\mathbb{P}_X(x)} \cdot \log P^{\zeta}(x, y)]$$
(1)の第二項を観ると、$$P_{X \mid \tilde{X}}^{\theta}(x \mid \tilde{x})$$は、$$\mathbb{P}_X$$のデータ生成分布へと収束するXの漸近的な周辺分布を有したエルゴード・マルコフ連鎖(ergodic Markov chain)となっている。したがって、(3)は次のように再記述できる。
$$\hat{\zeta} \approx \argmax_{\zeta} \lambda \sum_{i=1}^{n_s} \frac{\mathbb{Q}_X(x_i^s)}{\mathbb{P}_X(x_i^s)} \log P^{\zeta}(x_i^s, y_i^s) + (1 – \lambda)\sum_{i=1}^{n_t}[\log P_{X \mid \tilde{X}}^{\zeta}(x_j^t \mid \tilde{x}_j^t)] \tag{4}$$
(1)と(4)の差異は第一項のみである。重要なのは、もし$$\frac{\mathbb{Q}_X(x_i^s)}{\mathbb{P}_X(x_i^s)}$$が全ての$$x^s$$において定数ならば、$$\hat{\zeta}$$は$$\hat{\theta}$$に近似されるということである。実際、これが深層再構成分類ネットワークの目的関数となる。たとえ実践上一定の割合であるという想定があまりにも強固で成立しないとしても、(1)と(4)は$$\hat{\zeta}$$は$$\hat{\theta}$$の合理的な近似となり得ることを示している。
この関連から、教師なし学習の間にラベルなしのソースサンプルを利用したところでドメイン適応には影響を与えないという点に関しても明快となる。(4)の第一項は次のように拡張できる。
$$\lambda \sum_{i=1}^{n_s}\frac{\mathbb{Q}_X(x_i^s)}{\mathbb{P}_X(x_i^s)} \log P_{Y \mid X}^{\zeta}(y_i^s \mid x_i^s) + \lambda \sum_{i=1}^{n_s} \frac{\mathbb{Q}_X(x_i^s)}{\mathbb{P}_X(x_i^s)} \log P_X^{\zeta}(x_i^s)$$
上式の第二項を観れば、$$n_s \rightarrow \infty$$の時、$$P_X^{\theta}$$は$$\mathbb{P}_X^{\theta}$$へと収束する。したがって、
$$\int_{x \sim \mathbb{P}_X}^{} \frac{\mathbb{Q}_X(x)}{\mathbb{P}_X(x)} \log \mathbb{P}_X(x) \leq \int_{x \sim \mathbb{P}_X}^{} \mathbb{P}_X^t(x)$$
であるために、ラベルなしのサンプルを追加することによる影響は一定となる。このことが暗に示しているのは、一連の最適化の処理が(1)と等価になるということである。それは、ドメイン適応の文脈においては、ラベルなしのソースデータが無用(uselessness)であることを意味する。
尤も、以上の記述は、すなわちラベルなしのソースデータを組み合わせることが精度の劣化を伴わせるということを意味するのではない。深層再構成分類ネットワークが機能するのは、恐らく典型的な半教師あり学習と同様に、<教師あり学習>の内部で再帰的に再利用されている<教師なし学習>が<教師あり学習>の正則化として機能しているためである。
機能的等価物:PixelGAN
Bousmalis, K. et al.(2017)やWang, TC., et al. (2018)らの「敵対的生成ネットワーク(Generative Adversarial Networks: GAN)」の生成モデルを用いた「ドメイン適応(Domain Adaptation)」は、深層再構成分類ネットワークの機能的等価物と見做せる。深層再構成分類ネットワークと同じように、ここでのドメイン適応は、「教師なしドメイン適応」に他ならない。その主導的な差異は、ラベル付きサンプルが得られる「ソースドメイン(source domain)」とラベル付きサンプルが得られない、つまりラベル無しのサンプルしか得られない「ターゲットドメイン(target domain)」の区別で構成される。
しかしGANによるドメイン適応とDRCNによるドメイン適応は、ソースドメインにおけるラベル付きサンプルに関して区別される。GANによる教師なしドメイン適応は、ソースドメインにおけるラベル付きサンプルを条件付けGANのパラメタとして活用することで、ターゲットドメインにおけるラベル付きサンプルを生成することを可能にする。DRCNにおけるドメイン適応が、あくまでも再構成誤差最小化に基づいたラベル無しサンプルに対する学習に留まっていたのに対して、GANによるドメイン適応では、min-maxの最適化に基づくターゲットドメインの擬似的なラベル付きサンプルを学習することを可能にする。
ラベル付け担当者の負担軽減
この生成モデルを再利用すれば、より少ないラベル付きサンプルから、擬似的なラベル付きサンプルを増やすことが可能になる。ラベル付け担当者が用意すべきラベル付きサンプルの量も、相対的に減らすことが可能になる。
ソースドメインとターゲットドメインの区別は、観測クラスと未観測クラスの区別と同様に、相対的な差異に基づいている。ドメイン適応は、ソースドメインとターゲットドメインの区別を導入すると共に、ソースドメインの領域を徐々に拡張していくことにある。したがって、GANの生成モデルによる擬似的なラベル付きサンプルの生成処理は、理論的にはターゲットドメインにおける擬似的なラベル付きサンプルを生成していることになるものの、周り回ってソースドメインにおけるラベル付きサンプルを増やしていることに等しくなる。
GANのフレームワーク
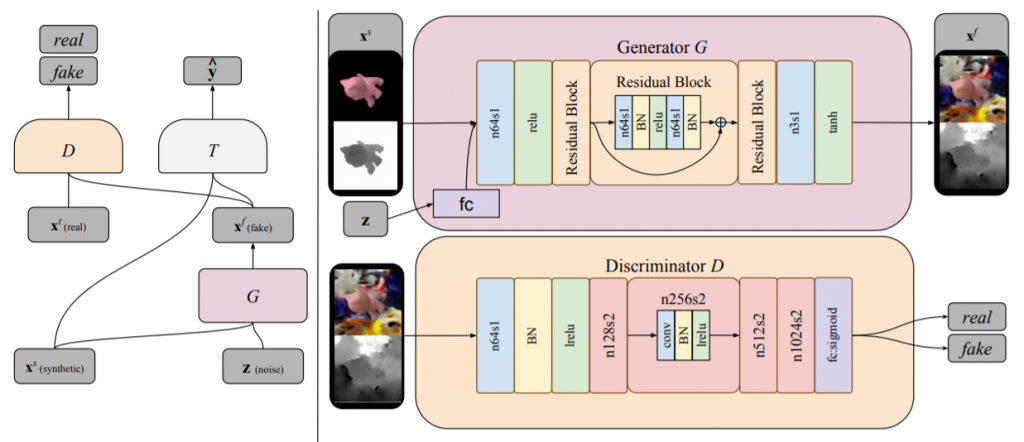
Bousmalis, K., Silberman, N., Dohan, D., Erhan, D., & Krishnan, D. (2017). Unsupervised pixel-level domain adaptation with generative adversarial networks. In Proceedings of the IEEE conference on computer vision and pattern recognition (pp. 3722-3731)., p3725より。
ターゲットドメインにおけるラベル付きサンプルを生成する生成器を$$G$$とする。訓練中、この生成器は $$G(x^s, z; \theta_G) \rightarrow x^f$$の特徴写像を実行する。ここで$$x^s$$はソースドメインにおけるサンプルを、$$z$$は入力ノイズのベクトルを、$$x^f$$は写像されたサンプルを、それぞれ表す。一方、識別器$$D$$は、尤度$$d$$を出力する$$D(x; \theta_D)$$の関数として表現できる。ここでの$$x$$は、この識別器に入力されるターゲットドメインにおけるサンプルか、生成器によって写像された$$x^f$$である。識別器の機能は、このターゲットドメインにおける「真の」サンプルと生成器によって生成された擬似的なサンプルを識別することである。尚、データ分布に関しては、「真の」ソースドメインの分布を$$X^t$$、生成器の写像の分布を$$X^f$$とする。
通常の条件付きGANの構成に加えて、Bousmalis, K. et al.(2017)のドメイン適応用のGANでは、更に、識別器と生成器にとって正則項として機能する分類器$$T$$が追加される。これは$$T(x; \theta_T) \rightarrow \hat{y}$$で、$$\hat{y}$$は$$x \in \{X^f, X^t\}$$に対応するラベルを表す。
最適化は、次のmin-maxの最適化となる。
$$\min_{\theta_G, \theta_T} \max_{\theta_D} \alpha \mathcal{L}_d(D, G) + \beta \mathcal{L}_t(G, T) \tag{1}$$
ここで、$$\alpha$$と$$\beta$$は各誤差の重みを表すトレードオフのパラメタである。$$\mathcal{L}_d$$は次のようなドメイン誤差(domain loss)を表す。
$$\mathcal{L}_d(D, G) = \mathbb{E}_{x^t}[\log D(x^t; \theta_D)] + \mathbb{E}_{x^s, z}[\log (1 – D(G(x^s, z: \theta_G); \theta_D))] \tag{2}$$
また$$\mathcal{L}_t$$はタスク特化型誤差(task-specific loss)で、典型的な分類問題同様、クロスエントロピー誤差となる。
$$\mathcal{L}_t(G, T) = \mathbb{E}_{x^s, y^s, z}[-{y^s}^T \log T(G(x^s, z; \theta_G);\theta_T) – {y^s}^T \log T(x^s);\theta_T] \tag{3}$$
ここで、$$y^s$$はラベルを表現するone-hotなベクトルを、$$x^s$$はソースドメインにおけるサンプルを、それぞれ表す。
画像分類や映像分類、行動認識問題の枠組みで言えば、ソースドメインとターゲットドメインの差異が、画角の微小変化や、人間が位置する場所や時間、立ち位置、僅かな姿勢の傾き加減によって生じているのならば、Bousmalis, K. et al.(2017)のContent-similarity lossは有用な誤差関数となる。
$$\min_{\theta_G, \theta_T} \max_{\theta_D} \alpha \mathcal{L}_d(D, G) + \beta \mathcal{L}_t(G, T) + \gamma \mathcal{L}_c(G) \tag{4}$$
ここで、$$\gamma$$は$$\alpha$$や$$\beta$$と同じように、トレードオフのパラメタとなる。また$$\mathcal{L}_c(G)$$は次のようなmasked-PMSEとして計算される。
$$\mathcal{L}_c(G) = \mathbb{E}_{x^s, z}[\frac{1}{k} \mid \mid (x^s – G(x^s, z; \theta_G)) \circ m \mid \mid_2^2 – \frac{1}{k^2}((x^s – G(x^s, z; \theta_G))^T m)^2] \tag{5}$$
ここで、$$m$$は二値(0-1)のマスクとなる。$$k$$はピクセルの個数を表す。また$$\mid \mid \cdot \mid \mid_2^2$$はL2ノルムに他ならない。
参考文献
- Ghifary, M., Kleijn, W. B., Zhang, M., Balduzzi, D., & Li, W. (2016, October). Deep reconstruction-classification networks for unsupervised domain adaptation. In European Conference on Computer Vision (pp. 597-613). Springer, Cham.
- Glorot, X., Bordes, A., & Bengio, Y. (2011). Domain adaptation for large-scale sentiment classification: A deep learning approach. In Proceedings of the 28th international conference on machine learning (ICML-11) (pp. 513-520).
- Goodfellow, I., Bengio, Y., & Courville, A. (2016). Deep learning (adaptive computation and machine learning series). Adaptive Computation and Machine Learning series, 800.
- Bousmalis, K., Silberman, N., Dohan, D., Erhan, D., & Krishnan, D. (2017). Unsupervised pixel-level domain adaptation with generative adversarial networks. In Proceedings of the IEEE conference on computer vision and pattern recognition (pp. 3722-3731).