問題設定:クラスタリングの正則化問題
画像認識、動画認識、行動認識のような大量の画像データセットを対象としたニューラルネットワーク最適化問題のためのノウハウは、しばしば画像を対象としたデータ・クラスタリングに応用されることがある。
浅い線形の関数を用いたクラスタリングのモデルは、データの非線形的な性質を十分には捕捉しない可能性がある。線形の関数は柔軟性に欠ける。また、しばしばこうした関数を使っていては、膨大なデータセットに対してスケールさせることが困難になる。
一方、深層学習に基づくクラスタリングは、非線形的で複合的かつ膨大なデータをモデル化する上で、十分な許容力を有している。しかし、こうした深層学習のクラスタリングでは、過剰適合(overfitting)の問題が避けられない。と言うのも、深層学習の無数のパラメタを訓練するための信頼できる教師データを用意することは困難であるためだ。
問題解決策:敵対的生成クラスタリングネットワーク
Ghasedi, K., et al. (2019)の「敵対的生成クラスタリングネットワーク(generative adversarial clustering network: ClusterGAN)」は、上記の問題を解決するために提唱された新しい深層学習に基づくクラスタリングのモデルである。ClusterGANは、クラスタリングのタスクのために導入された敵対的ゲームを採用している。そのアルゴリズムは、効率的に性能を向上させるための「自己学習アルゴリズム(self-paced learning algorithm)」として設計されている。
標準的なGANのネットワーク構造
標準的なGANのネットワーク構造は、識別器(discriminator)と生成器(generator)によって構成されている。特に、生成器Gは識別器Dを欺くために、アトランダムな入力zをデータ空間に写像することによって、真のデータを生成する。これに対して識別器は、真のデータを生成器によって生成された疑似的な真のデータから識別することを目的とする。したがって、生成器と識別器の敵対的ゲームにおける目的関数は次のようになる。
$$\min_G \max_D \mathbb{E}_{x \sim P(x)} [ \log D(x)] + \mathbb{E}_{z \sim P(z)} [\log (1 – D(G(z)))]$$
ここで、P(x)は、真のデータの分布を表わす。一方P(z)は生成器へのアトランダムな入力の分布を表わす。
ClusterGANのネットワーク構造
この典型的なGANのネットワーク構造とは異なり、ClusterGANのネットワーク構造は、三つのモデルによって構成されている。生成器Gと識別器Dに加えて、ClusterGANには「クラスタリングネットワーク(clustering network)」を意味する「クラスター器(Clusterer)」、Cが導入される。ここで、生成器とクラスター器は共に条件付き生成ネットワークとなる。一方でGは、潜在変数zを入力として受け取ることで疑似的なサンプルを次のように生成する。
$$G: z \rightarrow \hat{x}$$
他方でCは、この逆の変換を実行する。つまりクラスター器が生成するのは、生成器の入力となる潜在変数である。
$$C: x \rightarrow \hat{z}$$
識別器Dは、潜在変数と生成サンプルの同時確率分布を観測する。そしてDは、Gによって生成された$$(z, \hat{x})$$の組み合わせと$$(\hat{z}, x)$$の組み合わせを識別しようと試みる。
したがって、この敵対的ゲームにおいては、GとCが、共にDを欺くべく癒着した関係になる。
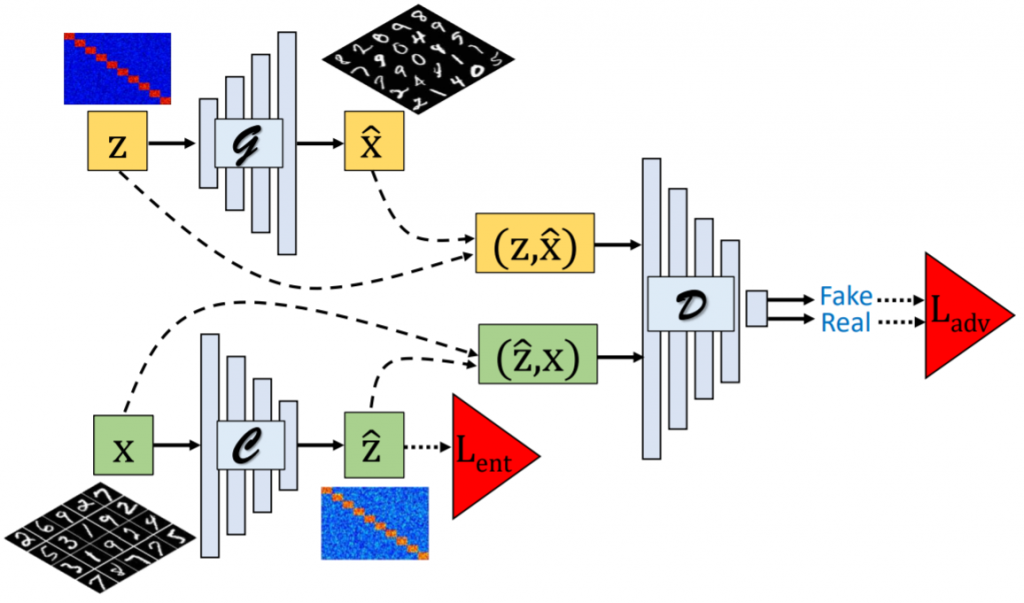
Ghasedi, K., Wang, X., Deng, C., & Huang, H. (2019). Balanced self-paced learning for generative adversarial clustering network. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (pp. 4391-4400)., p4394.
ブロック対角隣接行列のデータモデリング
ClusterGANでは、真の分布のサンプルを受け取ることで直接的に出力へと適用する目的関数が設計されている。そのためClusterGANのアルゴリズムは、その初期化戦略の一環として、真のデータから構成された隣接行列にブロック対角制約(block diagonal constraint)を加えるという発想を採る。
この制約を課すために、CluseterGANはまず、クラスター器の出力に適用されるコサイン類似度関数を用いて、真のサンプル間の類似度を計算する。そして、最小エントロピー誤差関数(minimum entropy loss function)によって、類似度を[0, 1]の範囲に規格化する。0ならば類似しておらず、1ならば類似していることを表す。
「自己学習アルゴリズム」
しかしながら、単なる教師なし学習では、真の類似度は未知に留まる。そのため、深層学習を用いたクラスタリングのモデルでは、上記の計算は原理的に困難になる。そこでClusterGANは、「自己学習アルゴリズム(self-paced learning algorithm)」を設計することで、この問題に対処している。
一般的に自己学習型のアルゴリズムは、複合性の低いサンプルで訓練過程を開始する。そしてその後に、より複合性の高いサンプルを徐々に訓練データに採り入れていく。誤差に基づいたサンプルの複合性を考慮するなら、自己学習は局所解で立往生する問題を緩和する――つまりモデルの汎化性能を高めることが知られている。
ClusterGANにおける自己学習型のアルゴリズムは、クラスター器の出力に基づいて、ブロック対角隣接行列Aを構築することを目的としている。ここで、
$$a_{ij} = 1 \ if \ y_i = y_j \ and \ a_{ij} = 0$$
適切なブロック対角隣接行列を実現すれば、複合性の高いクラスタリングのアルゴリズムを用いずとも、より単純なクラスタリングの割り当て(assignments)が可能になる。
クラスター器の出力層にはシグモイドの活性化関数が実装される。この出力に基づき、隣接行列は次のようなコサイン類似度関数によって計算される。
$$a_{ij} = \frac{\hat{z}_i^T\hat{z}_j}{\mid\mid \hat{z}_i\mid\mid\mid\mid \hat{z}_j \mid\mid}$$
ここで、$$\hat{z}_i$$はi番目のサンプルのクラスター器の出力を表す。
また、$$\mid\mid \cdot \mid\mid$$はl2ノルムの関数を表す。
ブロック対角隣接行列Aの構築を補佐するために、ClusterGANでは、直交または平行となるように、生成器へと入力される潜在変数zを初期化する。この初期化戦略においては、m/cの要素が1に等しく、その残りが0に等しくなる二値の確率変数が導入される。ここで、mはzのベクトルの長さを表す。この場合、クラスター器の出力の$$\hat{z}$$の分布がもし生成器の入力変数zと類似しているのならば、隣接行列をブロック対角として構造化させるという目的は達成することになる。
ただし、クラスター内の変動(variations)を表現するために、ClusterGANは生成器の入力に小さな一様ノイズを付加させる。経験的にこの初期化戦略のトリックは、より多様で現実的なサンプルを生成することに役立つと考えられる。言い換えれば、この一様ノイズは、クラスター器の正則化として機能する。
ClusterGANのミニマックスゲーム
敵対的ゲームの最中、ClusterGANの識別器は、生成器Gとクラスター器Cから受け取った次の二つの同時確率分布の識別を試みる。
$$P(z, \hat{x}) = P(z)P_G(x \mid z)$$
$$P(\hat{z}, x) = P(x)P_C(z \mid x)$$
真の分布に対応したP(x)とブロック対角隣接行列と一様ノイズによって構成されたP(z)の分布は、それぞれ既知である。したがって、ClusterGANの学習対象となるのは、$$P_G(x \mid z), P_C(z \mid x)$$の条件付き分布に他ならない。そしてこの学習において目指されるのは、$$P(z, \hat{x}), P(\hat{z}, x)$$の一致である。この条件を取得するために、CluseterGANのDは、GとCによって生成された二つの同時確率分布を識別するために学習する一方で、GとCは、Dの裏をかくべく、相互に類似した同時確率分布を生成するために学習する。したがってClusterGANの敵対的ゲームの価値関数は次のようになる。
$$\min_{G, C} \max_{D} U(D, G, C) = \mathbb{E}_{x \sim P(x)} [ \log D(C(x), x)] + \mathbb{E}_{z \sim P(z)} [ \log (1 – D(z, G(z)))]$$
この目的関数によって最適化されることで、識別器は、クラスタリングの分布と生成器の分布の属する組み合わせの結合分布の間でバランスを取ることができるようになる。
クラスタリングのエントロピー最小化
上述した敵対的誤差に加えて、CluseterGANでは、真のデータから構成された隣接行列に直接的に適用できるクラスタリングの誤差関数も設計されている。相互情報量の最大化や条件付きエントロピーの最小化は、クラスタリングの成功を表す結果として考えられる。ClusterGANにおけるクラスタリング問題では、この条件付きエントロピー最小化が次のように定式化される。
$$\min_C – \sum_{i, j = 1}^{n} [ a_{ij} \log a_{ij} + (1 – a_{ij}) \log (1 – a_{ij})]$$
ここで隣接行列$$a_{ij}$$は、0から1の範囲を取る。したがって、条件付きエントロピーの最小化は、ブロック対角隣接行列を追従する。しかしながら、クラスター器の出力結果から計算された類似度は、特に初期の訓練エポックにおいては不安定化してしまう。この不安定性に対処するために、CluseterGANでは、複合性の低いサンプルから徐々に複合性の高いサンプルに適合していく標準的な自己学習型のアルゴリズムを利用している。
$$\min_{C, \mathcal{v}}\sum_{i=1}^{n}v_il_i – \lambda_{\mathcal{v}} \sum_{i=1}^{n}v_i, \ s.t. \mathcal{v} \in [0, 1]^n$$
ここで、$$l_i = – \sum_{j=1}^n a_{ij} \log a_{ij} – (1 – a_{ij}) \log (1 – a_{ij})$$は、i番目のサンプルの誤差である。$$\mathcal{v}_i$$は自己学習型アルゴリズムの学習パラメタとなる。そして$$\lambda_v$$は学習ペースを制御するハイパーパラメタを表す。これらのパラメタは、クラスタリングと自己学習型アルゴリズムの訓練において、交互学習(alternative learning)の戦略を採る。
モデルのパラメタを固定した場合、自己学習型アルゴリズムのパラメタにおける大域最適解は、$$\mathcal{v}_i^{\ast} = 1 \ if \ l_i \lt \lambda_{\mathcal{v}} , \ \mathcal{v}_i^{\ast} = 0 \ otherwise$$となる。訓練中、$$\lambda_{\mathcal{v}}$$を増加させていけば、自己学習型アルゴリズムは訓練課程により複合的なサンプルを導入する。
しかしながら、標準的な自己学習型アルゴリズムでは、全クラスタから得られたサンプルのバランスを考慮した集合を選択することについては考慮されていない。そのためこのアルゴリズムは、ごく限られたクラスタにおいてでしか、複合性の低いサンプルを抽出しなくなる恐れがある。
そのためClusterGANでは、次のような目的関数を設計することで、多様性を欠如させた結果に対して罰則を与える仕組みを追加している。
$$\min_{C, \mathcal{v}} \sum_{k=1}^{c} \left[\sum_{i=1}^{n_k}v_{ki}(l_{ki}-\lambda_{\mathcal{v}})+\gamma\left(\sum_{i=1}^{n_k}\mid \mathcal{v}_{ki}\mid\right)^2\right] \ s.t. \mathcal{v} \in [0, 1]^n$$
ここで、$$\gamma$$は正則項のハイパーパラメタを表す。$$v_{ki}$$はi番目のサンプルに対するk番目のクラスタにおける自己学習のパラメタを表す。また、c個のクラスタに属すると想定されるデータは、$$\sum_{k=1}^{c}n_k = n$$となる。
上述した「バランスの取れた自己学習(balanced self-paced learning)」の目的関数は、二つの正則項を有している。
$$- \mid\mid \mathcal{v} \mid\mid_1 = – \lambda_{\mathcal{v}} \sum_{k=1}^c \sum_{i=1}^{n_k}v_{ki}$$
$$\mid\mid \mathcal{v} \mid\mid_e$$
第一の正則項は、より複合性の低いサンプルの選択を追従しているか否かに対応している。第二の正則項は、より多く選択されたサンプルを伴わせた集合に応じて罰則を与える正則化を実現している。つまり裏を返せば、この第二の正則項が表しているのは、サンプルの選択の多様性の低さに対する罰則となる。
したがって、これら二つの正則項により、「バランスの取れた自己学習」のアルゴリズムは、サンプルの抽出に対する複合性の低さと多様性の高さに裏打ちされた、ロバスト性の高さとバイアスの低さを追従する。
この目的関数を解決するために、CluseterGANは、クラスター器と自己学習型アルゴリズムにおける交互学習のアプローチを採用している。すなわち、一方のパラメタを固定した上で、他方のパラメタを更新していくアプローチである。クラスター器のパラメタを固定した場合、自己学習型アルゴリズムのパラメタの推定のための目的関数は次のようになる。
$$\min_{\mathcal{v}}\sum_{i=1}^{n}v_il_i – \lambda_{\mathcal{v}}\mid\mid\mathcal{v}\mid\mid_1 + \lambda\mid\mid\mathcal{v}\mid\mid_e \ s.t. \ \mathcal{v} \in [0, 1]^n$$
整合性誤差
敵対的誤差と最小エントロピー誤差に加えて、ClusterGANでは、「整合性誤差(consistency loss)」を利用したパラメタでも学習する。クラスター器は、一貫性の損失により、それぞれのサンプルとその変動に対して類似した出力を有するように促される。その際活用されるのは、以下のように、画像の変換処理とノイズである。
$$\min_C \sum_{i=1}^{n} \mid\mid C(x_i) – C(\hat{x}_i)\mid\mid^2$$
上述した最小エントロピー誤差関数は、フルバッチで定義されている。しかし、各ミニバッチのサンプルにのみ誤差を適用すれば、この拡張性の問題は実質的に解消される。
参考文献
- Ghasedi, K., Wang, X., Deng, C., & Huang, H. (2019). Balanced self-paced learning for generative adversarial clustering network. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (pp. 4391-4400).