問題設定: ラベルノイズ問題
機械学習の分類問題において、「ラベルノイズ(label noise)」は重要な派生問題になる。識別モデルの教師データとしてラベル付きサンプル(labeled samples)を用意する場合、ラベルを付与するのは、大抵の場合は人間となる。ラベルノイズという概念は、こうした人間によるラベル付けに起因した識別モデルの攪乱要因として位置付けられている。例えば一部のサンプルにのみ誤ったラベル付け(miss labeling)を施してしまえば、それは、予測精度の低下や必要な訓練データ数の増大など、分類の性能に対して多くの潜在的な悪影響を及ぼす。
Frénay, B., & Verleysen, M. (2013)らのラベルノイズ問題(Label noisy problem)では、ミスラベリングの問題が3つに区別されている。
- ラベルそれ自体の分布からも、データの分布からも独立した完全にアトランダムなノイズ(noisy completely at ranodom)。この場合、ミスラベリングという事象は一様分布に条件付けられて生起する。
- データに対して独立で、ラベルそれ自体の分布には独立したアトランダムなノイズ(noisy at random)。
- ラベルそれ自体の分布からも、データの分布からも、条件付けられて生起するアトランダムではないノイズ(noisy not at random)。
2.の例は医療分野の、特に被験者のバイタルデータなどのように、ラベルを入手すること自体に困難さが伴い、しばしば厳密なラベリングができない場合に該当する。3.の例は、異なるラベルのように思えても、データの特徴点の類似性が高い場合に該当する。例えば猫と犬の識別よりも、猫と山猫の識別のほうが、このミスラベリングは生起し易い。
問題再設定: ニューラルネットワーク最適化問題としてのラベルノイズ問題
ニューラルネットワークに限定して言えば、ラベルノイズに対してロバスト性を備えた誤差関数は、主に二値分類(binary classification)の問題との関連から設計されてきた。二値論理構造において、あるラベルを別のラベルとして設定してしまうことに起因するラベルノイズ問題の事象は、正を負に、負を正に逆転(flip)させてしまう事象に等しい。そのためこの問題領域では、ラベルノイズ問題は「ラベルフリップ(label filp)」の問題として(再)記述されている。そしてこの二値論理構造で養われた誤差関数は、後に多値論理構造、すなわち多クラス分類へも拡張されている。
Natarajan, N, et al., (2013)は、ラベルフリップによって識別の精度が劣化することを総じて「リスク(risk)」と呼んでいる。ラベルノイズへの対策は、総じてこの「リスクの最小化(risk minimization)」として設定できる。
以上の概念史を前提とすれば、ラベルノイズに対するロバスト性を備えた誤差関数に対する機能的な比較は、この「リスクの最小化」を可能にしているニューラルネットワーク最適化アルゴリズムの機能的な比較によって成立することがわかる。
問題解決策: 不偏推定量の逆伝播
Natarajan, N, et al., (2013)はまず、真の分布についての一切の知識や想定を持たずに、一様のランダムノイズの下でのリスク最小化を試みた。そして確率的最適化の知見から、誤差関数の不偏推定量を以って補正された誤差を、ラベルノイズありのラベルの学習において使用した。この補正された誤差は、各ラベルに依存した値となるものの、一定の閾値範囲に収まる単純な重み付けで構わないとされる。
ノイズ行列$$T$$を正則行列とする。誤差$$l$$が得られた時、逆伝播される補正済み誤差は次のように定義される。
$$l^{\leftarrow}(\hat{p}(y \mid x)) = T^{-1}l(\hat{p}(y \mid x))$$
ここで、$$x$$は訓練データを、$$y$$はラベルを、$$\hat{p}$$は確率分布を、それぞれ表す。
誤差の補正は不偏である。すなわち、ノイズの孕んでいるラベルを$$\tilde{y}$$とするなら、
$$\forall x, \mathbb{E}_{\tilde{y}\mid x}l^{\leftarrow}(y, \hat{p}(y \mid x)) = \mathbb{E}_{y\mid x}l(y, \hat{p}(y \mid x))$$
したがって、
$$\mathbb{E}_{\tilde{y}\mid x}l^{\leftarrow}(y, \hat{p}(y \mid x)) = \mathbb{E}_{y \mid x}Tl^{\leftarrow}(\hat{p}(y \mid x)) = \mathbb{E}_{y \mid x}TT^{-1}l(\hat{p}(y \mid x)) = \mathbb{E}_{y \mid x}l(\hat{p}(y \mid x))$$
であるため、これらの最小化もまた等価となる。
$$\newcommand{\argmin}{\mathop{\rm arg~min}\limits} \argmin_{\hat{p}(y \mid x)} \mathbb{E}_{x, \tilde{y}}l^{\leftarrow}(y, \hat{p}(y \mid x)) = \argmin_{\hat{p}(y \mid x)}\mathbb{E}_{x, y}l(y, \hat{p}(y \mid x))$$
補正された誤差は各観測ラベルにおける誤差の値の線型結合となる。その係数は、$$T^{-1}$$が、観測された$$\tilde{y}$$によって得られるそれぞれの真のラベル$$y$$に割り当てる確率に対応する。直観的(Intuitively)に言えばこれは、マルコフ連鎖$$T$$によって記述されるノイズ過程において、一ステップ分後退することを意味する。補正された誤差は、それが常に非負でなくても、微分可能である。それ故にそれは逆伝播によって最小化することができる。
問題解決策: ラベル遷移確率行列の順伝播
後にPatrini, G., et al. (2017)が指摘したように、Natarajan, N, et al., (2013)らの特殊な誤差関数を使用したラベルノイズ対策は、逆伝播に関連する最適化アルゴリズムとして位置付けられる。ニューラルネットワーク最適化問題の枠組みでは、逆伝播に関連する最適化は、常に順伝播と関連している。Patrini, G., et al. (2017)が順伝播からのアプローチとして位置付けているSukhbaatar, S., et al. (2014)のモデリングでは、Natarajan, N, et al., (2013)同様、ラベルフリップが次のようにモデル化されている。
$$p(\tilde{y} = j \mid x) = \sum_{i}^{}p(\tilde{y} = j \mid y^{\ast} = i)p(y^{\ast} = i \mid x) = \sum_{i}^{}q_{ji}^{\ast}p(y^{\ast} = i \mid x) \tag{1}$$
ここで、$$(x_n, y_n^{\ast})$$は訓練データ集合である。$$y^{\ast}$$は$$\in 1, …, K$$から成る真のラベルを表す。ラベルノイズを孕んだラベルは$$\tilde{y}$$は、$$K \times K$$の確率繊維行列$$Q^{\ast} = (q_{ji}^{\ast})$$によってパラメタ化される確率分布$$p(\tilde{y} = j \mid y^{\ast} = i) = q_{j, i}^{\ast}$$から得られる。
確率行列$$Q$$を使えば、ノイズが孕んだラベル付きサンプルのラベル分布と適合するように識別モデルを再記述することができる。識別モデルによる真のラベルの予測確率を$$\hat{p}(y^{\ast} \mid x, \theta)$$とするなら、識別モデルは次のような組み合わせになる。
$$\hat{p}(\tilde{y} = j \mid x, \theta, Q) = \sum_{i}^{}q_{ji}\hat{p}(y^{\ast} = i \mid x, \theta) \tag{2}$$
このモデルは、$$\theta$$によってパラメタ化されているベースモデル(base model)と$$Q$$によってパラメタ化されているノイズモデル(noise model)に分解することができる。これら2つのモデルによって構成されている上記のモデルは、ノイズラベル$$\tilde{y}$$と式(2)によって得られる予測確率のクロスエントロピーを最大化することによって訓練される。したがってそのコスト関数は、次式を最小化することになる。
$$\mathcal{L}(\theta, Q) = -\frac{1}{N}\sum_{n=1}^{N}\log \hat{p}(\tilde{y} = \tilde{y}_n \mid x_n, \theta, Q) = – \frac{1}{N} \sum_{n=1}^{N} \log \left(\sum_{i}^{} q \tilde{y}_n i \hat{p}(y^{\ast} = i \mid x_n, \theta)\right) \tag{3}$$
ここで、$$N$$は訓練データの件数を表す。しかし、最終的な目標は、真のラベル$$y^{\ast}$$を予測することであって、ラベルノイズを孕んだラベル$$\tilde{y}$$ではない。これを成し遂げるには、ベースモデルが真のラベルを予測できるように調整しなければならない。その一つの方法となるのは、次のように定義される混合行列(confusion matrix)$$C = \{c_{ij}\}$$を利用することである。
$$c_{ij} := \frac{1}{\mid S_j \mid}\sum_{n \in S_j}^{} \hat{p} (y^{\ast} = i \mid x_n, \theta)$$
ここで、$$S_j$$は真のラベル$$y^{\ast} = j$$を持つ訓練データの集合を表す。もしこの混合行列が単位行列になるように制御できれば、ベースモデルは完全に訓練データの真のラベルを予測していることになる。ただし注意しなければならないのは、これはノイズモデルによる調整が介在する以前の予測であるという点だ。ベースモデルとノイズモデルの組み合わせを前提とした場合、その交差行列$$\tilde{C} = \{\tilde{c}_{ij}\}$$は次のように再記述される。
$$\tilde{c}_{ij} := \frac{1}{\mid S_j \mid}\sum_{n \in S_j}^{}\hat{p}(\tilde{y} = i \mid x_n, \theta, Q) \tag{5}$$
式(2)より、$$\tilde{C} = QC$$である。だが現実的に$$C$$と$$\tilde{C}$$を測定するためには、真のラベルを知っておかなければならない。そこで重要となるのは、式(3)の目的関数の最小化が、ベースモデルとノイズモデルの組み合わせモデルによる予測分布を、訓練データにおけるノイズラベル分布に可能な限り近接させようとしている点である。$$N \rightarrow \infty$$の時、式(3)の目的関数は次のようになる。
$$\mathcal{L}(\theta, Q) = – \frac{1}{N}\sum_{n=1}^{N}\log \hat{p}(\tilde{y} = \tilde{y}_n \mid x_n) = -\frac{1}{N}\sum_{k=1}^{K}\sum_{n \in S_k}^{} \log \hat{p}(\tilde{y} = \tilde{y}_n \mid x_n, y_n^{\ast} = k)$$
$$\xrightarrow{N \rightarrow \infty} – \sum_{k=1}^{K}\sum_{i=1}^{K}q_{ik}^{\ast}\log\hat{p}(\tilde{y} = i \mid x, y^{\ast} = k) \geq – \sum_{k=1}^{K}\sum_{i=1}^{K}q_{ik}^{\ast}\log q_{ik}^{\ast} \tag{6}$$
ここで、$$- \sum_{k}^{}q_k^{\ast} \log \hat{p}_k \geq -\sum_{k}^{}q_k^{\ast}\log q_k^{\ast}$$である。また式(6)の等号が成り立つのは$$\hat{p}(\tilde{y} = i \mid x, y^{\ast} = k) = q_{ik}^{\ast}$$の場合に限られる。言い換えれば、上記の組み合わせモデルが試行しているのは、組み合わせモデルの交差行列$$\tilde{C}$$をラベルノイズの真のノイズ分布$$Q^{\ast}$$に適合させるということである。すなわち、
$$\tilde{c}_{ik} = \frac{1}{\mid S_k \mid} \sum_{n \in S_k}\hat{p}(\tilde{y} = i \mid x_n, y_n^{\ast} = k) \rightarrow q_{ik}^{\ast} \Rightarrow \tilde{C} = QC \rightarrow Q^{\ast} \tag{7}$$
もし真のノイズ分布$$Q^{\ast}$$が既知であって、それが正則行列であるなら、式(7)より、$$Q = Q^{\ast}$$として設定することで、$$C$$を単位行列へと収束させることになる。したがって、$$Q^{\ast}$$によってパラメタ化されている組み合わせモデルを利用することで、ノイズの孕んだラベルを予測するべく訓練すれば、それが直接的に、ベースモデルが真のラベルを予測するように訓練したことになる。
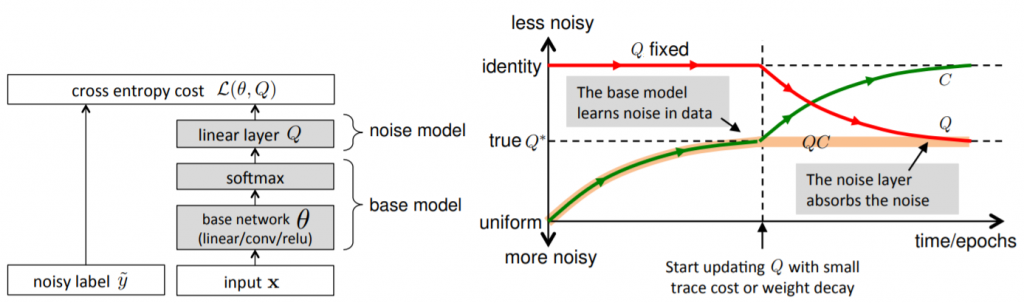
Sukhbaatar, S., Bruna, J., Paluri, M., Bourdev, L., & Fergus, R. (2014). Training convolutional networks with noisy labels. arXiv preprint arXiv:1406.2080., p3より掲載。
画像認識や動画認識の場合、ベースモデルとなるのは、出力層にsoftmax層を備えた畳み込みニューラルネットワークである。ノイズモデルは入出力の次元が共に$$K$$の全結合層となる。つまり$$K \times K$$の重み行列のみをパラメタとして持つ線形変換のみを担う。
しかし、真のノイズ分布$$Q^{\ast}$$は実用上未知である場合が多い。特に(統計的)機械学習の非専門家であるエンドユーザーがラベル付けを実践する場合には、真のノイズ分布は設計時点では不確実である。
この場合、ノイズを孕んだデータそれ自体から、真のノイズ分布を推論しなければならない。だが幸いなことに、ノイズモデルは線形変換に過ぎない。それはその重み行列となる$$Q$$が、他のネットワークとの関連から更新され得るということである。そのパラメタの更新は、$$Q$$の行列を通じたクロスエントロピーの誤差をベースモデルへと逆伝播することで進行する。しかし残念なことに、式(3)における誤差を単純に最小化することは困難である。式(6)より、訓練過程を通じて、$$QC = \tilde{C} \rightarrow Q^{\ast}$$となる。$$\tilde{C}$$は組み合わせモデルにおける交差行列で、$$Q^{\ast}$$はデータにおける真のノイズ分布である。しかしながら、これ単独では$$Q \rightarrow Q^{\ast}$$や$$C \rightarrow I_K$$が保証されない。
Sukhbaatar, S., et al. (2014)は、$$Q \rightarrow Q^{\ast}$$を保証するために、確率行列$$Q$$に対して、行列の対角和を用いた正則項を追加している。この正則項は、ラベルノイズをベースモデルからノイズモデルへと効果的に転移させることを可能にする。それにより、$$Q \rightarrow Q^{\ast}$$の収束を保証するのである。
$$tr(Q^{\ast}) = tr(QC) = \sum_{i}\left(\sum_{j}^{}q_{ij}c_{ji})\right) = \sum_{i}^{}q_{ii}\left(\sum_{j}^{}c_{ji}\right) = \sum_{i}^{}q_{ii} = tr(Q)$$
$$tr(Q^{\ast})$$は$$tr(Q)$$の下限である。そして上記の等号は、$$C = I_K$$かつ$$Q = Q^{\ast}$$の場合にのみ成り立つ。したがって、$$tr(Q)$$の最小化は、ベースモデルがクリーンなラベルを正確に予測するために機能する。$$Q$$はノイズモデルにおける重み行列のパラメタである。故に、ニューラルネットワーク最適化問題においては、$$tr(Q)$$の最小化は重み減衰のような正則化によって間接的に成し遂げることができる。
問題解決策: ラベル遷移確率行列の初期化戦略および転移学習
Patrini, G., et al. (2017)は、Natarajan, N, et al., (2013)における逆伝播のアルゴリズムとSukhbaatar, S., et al. (2014)における順伝播のアルゴリズムが、両立可能であることを指摘した。確かに、Sukhbaatar, S., et al. (2014)のノイズモデルの重み行列$$Q$$は、Natarajan, N, et al., (2013)の補正済み誤差によって更新することが可能である。Sukhbaatar, S., et al. (2014)は$$Q$$の初期値を単位行列として想定していたが、Natarajan, N, et al., (2013)の補正済み誤差の逆伝播によって予め$$T$$のパラメタの事前学習(pre-learning)を実行しておけば、それによって得られる$$T$$は、より$$Q^{\ast}$$に近い$$Q$$として転移させることができる。
Patrini, G., et al. (2017)の学習アルゴリズムは、Sukhbaatar, S., et al. (2014)が導入したベースモデルとノイズモデルの区別に準拠すれば、end-to-endとして実現可能である。それ故にこの学習アルゴリズムは、次のような学習の方向付けを与えている。
- ベースモデル単体を対象とした補正なしの誤差による最適化。
- ノイズモデルと組み合わせたベースモデルを対象とした補正済み誤差による最適化。
- 2. の事前学習結果を用いた転移学習。2.の学習結果として得られる更新済みの$$Q$$を改めて2. のモデルに転移させることで実現する。
参考文献
- Frénay, B., & Verleysen, M. (2013). Classification in the presence of label noise: a survey. IEEE transactions on neural networks and learning systems, 25(5), 845-869.
- Goodfellow, I., Bengio, Y., & Courville, A. (2016). Deep learning (adaptive computation and machine learning series). Adaptive Computation and Machine Learning series, 800.
- Natarajan, N., Dhillon, I. S., Ravikumar, P. K., & Tewari, A. (2013). Learning with noisy labels. In Advances in neural information processing systems (pp. 1196-1204).
- Patrini, G., Rozza, A., Krishna Menon, A., Nock, R., & Qu, L. (2017). Making deep neural networks robust to label noise: A loss correction approach. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (pp. 1944-1952).
- Sukhbaatar, S., Bruna, J., Paluri, M., Bourdev, L., & Fergus, R. (2014). Training convolutional networks with noisy labels. arXiv preprint arXiv:1406.2080.
- Wilson, D. R., & Martinez, T. R. (1997, July). Instance pruning techniques. In ICML (Vol. 97, No. 1997, pp. 400-411).