移動体検知の「照明」変化脆弱性対策

問題設定：移動体検知の照明変化

移動体検知(Moving object detection: MOD)は、画像の系列から移動体を抽出する処理を指す。このモデルは主に、空港、住宅地、ショッピングモール、交通網のビデオ監視などに応用されているコンピュータビジョン、物体追跡(object tracking)、また人間とマシンの相互行為のための身振りの認識(gesture recognition)にとって、基礎的なタスクとして知られている。様々なモデルがこれまで提唱されてきたが、そのいずれも照明(illumination)の変化に対しては脆弱であった。

移動体検知問題の解決策として、ガウス混合モデルやカーネル密度推定などのような従来の統計的方法においては、背景のピクセル強度をモデル化した上で、各フレームのピクセルを比較することで前景を検知してきた。より最先端(state-of-the-art)として知られている方法としては、低ランクのスパース行列分解に基づいた解決策がある。こうした解決策では、背景のピクセルが画像の系列で時間的に相互に線形に相関しているという事実を利用することで、主成分分析の変異体(variant)を適用し、背景と疎な外れ値に関する低ランク表現を抽出していく。しかし、これらの統計的な方法に基づく解決策は、照明の変化を主題とした対策は講じていない。

問題再設定：再構成誤差最小化問題としての移動体検知問題

照明の変化は、表現学習においては正則化によって処理されるべき対象とも考えられる。移動体検知問題における照明の変化は、その大部分が背景の変化として結実する。照明に照らされている移動体の表層部分は、微かに色調が変異するであろう。移動体検知器に求められるのは、こうした照明の変化に伴う背景の大幅な変異を外れ値として無視すると共に、前景の微弱な色調の変化を汎化するような学習である。

これを前提とするなら、移動体検知問題をニューラルネットワーク最適化問題として再設定することは、実り多き発見をもたらす。事実ニューラルネットワーク最適化問題の枠組みの中でも、コンピュータビジョンとの関連から多くの前景検知器が提案されてきた。

しかしながら、大多数のニューラルネットワークは移動体に関するピクセル単位での教師データを必要としてしまう。単なる画像分類とは異なり、移動体検知の教師あり学習となれば、ラベル付きサンプルの配備に多大なコストを要してしまう。単なる「物体検知(object detection)」ならば、このラベル付けのコストは限定的であったであろう。しかし移動体検知となるならば、物体の位置関係のみならず、その時系列的な推移を観察しながらラベルを付与していかなければならない。

物体検知や教師あり学習に多大な情熱を捧げる者でもない限りは、多くの場合、このラベル付けコストは割に合う投資とはなり得ない。現実的なアプリケーションの現場においては、教師なし学習による最適化が現実的な問題解決策として要求されている。したがって我々は、ニューラルネットワーク最適化問題としての移動体検知問題を自己符号化器(Auto-Encoder)の再構成誤差最小化問題として再設定した上で、個々の問題解決策を比較していく。

問題解決策：深層背景学習

「動的な背景から前景を検出することは、困難な課題である。何故なら、綺麗な背景画像の集合を発見することが非常に困難で、背景もまた動的に変異するからである。前景が消失している時か、映像系列の中で発生している時に、映像のフレームにおける幾つかの部分は綺麗な背景となる。そのため、ほとんどの時間において、ピクセルは背景に属する。これは、我々の研究の基本的な観察である。」

Xu, P., Ye, M., Li, X., Liu, Q., Yang, Y., & Ding, J. (2014, November). Dynamic background learning through deep auto-encoder networks. In Proceedings of the 22nd ACM international conference on Multimedia (pp. 107-116). ACM., p108.

Xu, P., et al. (2014)で提案されているモデルでは、二つの自己符号化器をスタックした構造として設計されている。二つの自己符号化器をスタックさせているのは、理由のないことではない。このモデルでは、第一の自己符号化器が「背景抽出ネットワーク(Background Extraction Network)」として機能するのに対して、第二の自己符号化器は「背景学習ネットワーク(Background Learning Network)」として機能する。

Xu, P., Ye, M., Li, X., Liu, Q., Yang, Y., & Ding, J. (2014, November). Dynamic background learning through deep auto-encoder networks. In Proceedings of the 22nd ACM international conference on Multimedia (pp. 107-116). ACM., p109.

この自己符号化器は、事前に背景情報に関して学習した後に、背景と前景の差異を推論するモデルとなっている。

自己符号化の構造

「背景抽出ネットワーク」に入力される観測データ点は、グレースケールに変換された画像のピクセル値を一次元にflattenした１次元のベクトルとなる。値は0-256から0-1にスケールされている。その際、映像の各フレームは次のように表現される。

$$\vec{x} = \{x^1, x^2, …, x^D\} \ (x^j \in [0, 1]^N)$$

ここで$$D$$はフレーム数を意味する。$$N$$は1フレームにおけるピクセル数を意味する。この集合 $$\vec{x}$$ が、「背景抽出ネットワーク」への入力データとなる。一方、「背景抽出ネットワーク」からの出力データは、次のようになる。

$$B^0 \in [0, 1]^N$$

次の$$h_1$$ と $$h_2$$ は、それぞれの符号化の段階で出力された値である。

$$h_1 = f(x) = sigm(W_{1}x ＋ b_1)$$
$$h_2 = f(h_1) = sigm(W_{2}h_1 ＋ b_2)$$

ここで、$$f$$は特徴変換の関数で、$$sigm$$はシグモイド関数ないしロジスティクス関数を意味する。$$W_{1}x$$ と $$W_{2}h_1$$ はそれぞれ、Encoderにおける第一と第二の重み行列を表す。$$b_N$$ は N層目のバイアスのベクトルを表す。復号化の段階での出力は次のようになる。

$$h’_1 = g(h_2) = sigm(W^T_2 h_2 ＋ b_3)$$

再構成の特徴点(feature points)は次のようになる。

$$\vec{\hat{x}} = g(h’_1) = sigm(W^T_1 h’_1 ＋ b_4)$$

最小化すべきコスト関数は典型的なクロスエントロピーとなっている。

$$\epsilon (\vec{x}) = – \sum_{i=1}^{N}(\vec{x}_i \log \hat{\vec{x}}_i ＋ (1 – \vec{x}_i) \log (1 -\hat{\vec{x}}_i))$$

コスト関数の設計

ここまでの記述は全く何も新しくない。

むしろ特筆すべきなのは、論文でも明記されている通り、「テクニカルに設計されたコスト関数(a technically designed cost function)」(Xu, P., et al. 2014, p108.)である。「背景抽出ネットワーク」の出力は、「背景学習ネットワーク」の入力となる。しかし両者の中継点には、次のような分離機能／関数(separation function)が導入されている。

$$S(\hat{\vec{x}}_i^j, B_i^0) \ (i = 1, 2, …, N)$$

二つの復号化の層を仮定するなら、この分離関数の出力はそれぞれ$$h_{B_1}$$ と $$h_{B_2}$$ となる。また、符号化と再構成の層の出力はそれぞれ $$h’_1$$ と $$\hat{\vec{B}}$$ と表せる。

この特殊なコスト関数を導入するにあたり、Xu, P., et al. (2014)は、「前景」と「背景」の区別を「クリーンなデータ(clean data)」と「ノイズのデータ(noise data)」の区別で展開している。ここからこのモデルはノイズ除去型自己符号化(Denoising Auto-encoder)の発想に近付いていく。つまりこのモデルの学習は、「前景」と「背景」の混成によって成り立つ観測データ点をノイズありの観測データ点として学習していくアルゴリズムと論理的に等価となる。

「第一の自己符号化器は、『クリーンな』背景画像および各ピクセルの背景の変動の許容範囲を学習するノイズ除去型の自己符号化器のように働く。許容度は、最初のDフレームの各々の背景画像を得るために有用となる。L1の最適化を利用することで、フレームをBを適合するだけでは、良好な結果は得られない。抽出された背景画像には前景が含まれている。深層アーキテクチャは、背景のより不変な表現を学習する。これにより、『クリーンな』背景画像をより良く再構成することで、前景を除去することを可能にする。我々のアルゴリズムはよりロバストになり得る。」

Xu, P., Ye, M., Li, X., Liu, Q., Yang, Y., & Ding, J. (2014, November). Dynamic background learning through deep auto-encoder networks. In Proceedings of the 22nd ACM international conference on Multimedia (pp. 107-116). ACM., p110.

「背景抽出ネットワーク」のコスト関数は次のように定義される。

$$\newcommand{\argmax}{\mathop{\rm arg~max}\limits} \newcommand{\argmin}{\mathop{\rm arg~min}\limits} \min_{\theta_E, B^0, \sigma} \it{L}(\vec{x}^j; \theta_E, B^0, \sigma) = \epsilon (\vec{x}^j) ＋ \sum_{i=1}^{N}\mid\frac{\vec{x}_i^j – B^0}{\sigma_i}\mid ＋ \lambda \sum_{i=1}^{N}\mid \sigma_i \mid$$

ここで、 $$j$$ はフレーム番号を表す。$$N$$は次元を表す。$$\lambda$$ は調整可能なハイパーパラメタで、$$0 < \lambda < 1$$ となる。
上記のコスト関数において、$$B^0$$ は、背景画像の特徴表現となるパラメタを表す。$$\sigma$$ は$$B^0$$ の許容値(tolerance value)を表す。背景のピクセルが変われば、この値も変わる。また、$$\theta_E = W_{E_i} \ (i = 1, 2)$$ で、 $$\ b_{E_i} (j = 1, …, 4)$$となる。

上記コスト関数第二項では、大きな分散に対して弾力性を持たせるために、i番目のピクセルでパラメタ$$\sigma_i$$の近似誤差を除算することになる。上記のコスト関数の第三項は正則化の用途で導入されている。

コスト関数の最適化アルゴリズム

「背景抽出ネットワーク」の学習では、$$\theta_E$$、$$B^0$$、そして$$\sigma$$の訓練が同時に実行される。パラメタ $$\theta_E$$ は、「背景抽出ネットワーク」の重み行列とバイアスベクトルを表している。学習率を $$\eta$$ とするなら、その更新処理は次のようになる。

$$\theta_E = \theta_E – \eta \Delta \theta_E$$

ここで、偏微分は次のように定式化される。

$$\Delta \theta_E = \frac{\partial \it{L} (\theta_E, B^0, \sigma)}{\partial \theta_E} = \frac{\partial \epsilon (\vec{x}^j)}{\partial \theta_E} ＋ \frac{\partial \left(\sum_{i=1}^{N}\mid\frac{\vec{x}_i^j – B_i^0}{\sigma_i}\mid\right)}{\partial \theta_E}$$

右辺第二項は微分可能ではないため、Xu, P., et al. (2014)ではそのderivativeを荒く計算するために、ここでは符号関数(sign function)が導入されている。

$$\Delta \theta_E = \frac{\partial \epsilon (\vec{x}^j)}{\partial \theta_E} ＋ \sum_{i=1}^N sign \left(\frac{\vec{x}_i^j – B_i^0}{\sigma_i}\right)\frac{\partial \hat{\vec{x}}_i^j}{\partial \theta_E}$$

$$\theta_E$$ の更新処理を前提とすれば、 $$B^0$$ の最適化問題は次の最小化問題と論理的に等価となる。

$$\sum_{i=1}^N \left(\min_{B_i^0} \sum_{j=1}^D\mid \hat{\vec{x}}_i^j – B_i^0 \mid\right)$$

この最小化問題は、粒度を細かくすれば、次のように再記述できる。

$$\min_{B_i^0} \sum_{j=1}^D\mid \hat{\vec{x}}_i^j – B_i^0 \mid \ (i = 1, 2, …, N)$$

L1正規化により、最適な $$B_i^0$$ は、 $$\{\hat{\vec{x}}_i^1, …, \hat{\vec{x}}_i^D\}$$ の中央値と同値となる。

$$\theta_E$$ と $$B^0$$ が更新された後の$$\sigma_i$$におけるコスト関数は次のように再記述できる。

$$\it{L}(\sigma_i) = \mid \frac{\hat{\vec{x}}_i^j – B_i^0}{\sigma_i}\mid ＋ \lambda \mid \sigma_i \mid$$

この最適化はその対数形式の最小化と等価となる。$$\ln \it{L}(\sigma_i)$$のderivativeが $$0$$ になるべく再度定式化するなら、次のように再記述できる。

$$\frac{\partial \ln \it{L}(\sigma_i)}{\partial \sigma_i} = \frac{2 \lambda \sigma_i}{\lambda \sigma_i ＋ \mid \hat{\vec{x}}_i^j – B_i^0 \mid} – \frac{1}{\sigma_i} = 0$$

最適な $$\sigma_i$$ は次のようになる。

$$\sigma_i^{\ast} = \sqrt{\mid\frac{\hat{\vec{x}}_i^j – B_i^0}{\lambda}\mid}$$

ミニバッチ学習では、D枚のフレームごとにこの最適値を計算し、その加算平均値をそのバッチの最適値とする。

分離関数／機能の定義

以上の最適化処理を前提とすれば、分離機能／関数となる $$S$$ に具体的な定義を与えることが可能になる。

$$B_i^j = S(\hat{\vec{x}}_i^j, B_i^0) =
\begin{cases}
\hat{\vec{x}}_i^j \ (\mid \hat{\vec{x}}_i^j – B_i^0\mid \leq \sigma_i) \\
B_i^0 \ (\mid \hat{\vec{x}}_i^j – B_i^0\mid > \sigma_i)
\end{cases}
$$

「背景学習ネットワーク」の最適化

「背景学習ネットワーク」の最適化は以下のように定式化される。

$$\it{L}(B^J, \theta_L) = – \sum_{i=1}^N (B_i^j \log \hat{B}_i^j ＋ (1 – B_i^j)\log (1 – \hat{B}_i^j))$$

この最適化には勾配降下法が用いられる。

「排除された第三項」としての照明変化

このモデルは非線形の背景モデルを構築する。しかし、照明の変化に対応することはできない。上述した通り、「テクニカルに設計されたコスト関数(a technically designed cost function)」によって、「背景抽出ネットワーク」と「背景学習ネットワーク」の中継点には、分離機能／関数(separation function)が導入される。そしてこのアルゴリズムでは、「前景」と「背景」の区別が「クリーンなデータ(clean data)」と「ノイズのデータ(noise data)」の区別で展開される。

しかし、このように区別を導入した場合、照明の変化がこの区別のどちらの側に位置付けられるのかが不透明になる。時系列のパターンとして観るなら、照明の変化が生じたフレームは、外れ値のようなもので、ノイジーでもある。故にモデルは、照明の変化が生じたフレームを「ノイズのデータ」として観察するかもしれない。

だが照明の光は、照明と移動体との間の障害物を仮定しないならば、前景と背景の双方に行き届くはずだ。だとするとこの場合、モデルによって「ノイズのデータ」として観察されるのは、我々が「前景」として認識している移動体と本来の意味での「背景」の双方であるということになる。しかしながらモデルはフレームの全域を「ノイズのデータ」として観察するのだから、モデルの観点では、「前景」と「背景」の差異は消失してしまう。結果的にノイズ除去型の自己符号化器として機能するXu, P., et al. (2014)のモデルは、このフレームから、全てのピクセル領域を「前景」として検知してしまう。それ故に推論される「背景」は、「前景」も「背景」も無い、言わば「空」となる。

論理学的に言えば、照明の変化は、「前景」と「背景」の区別を導入したことによって派生する「排除された第三項」である。照明の変化は、「前景」と「背景」の区別の二値論理構造を破綻させる。「前景」と「背景」の区別が二値論理として機能し続けるためには、照明の変化を無視し続けなければならない。これを前提とすれば、この深層背景学習が機能するのは、照明の変化を盲点として位置付けておき、この盲点が決して暴露されない限りにおいてのこととなる。

問題解決策：教師なしニューラル移動体検知

Bahri, F., et al.(2018)が提案した「教師なしニューラル移動体検知(Neural Unsupervised Moving Object Detection: NUMOD)」は、Xu, P., et al. (2014)の盲点としての照明変化を初めから埋め合わせるべく設計されている。このモデルでは、「前景」と「背景」の区別を導入するのではなく、「前景」となる「移動体」と「背景」と「照明変化(illumination changes)」の区別を導入している。二値論理ではなく多値論理を前提としたこのモデルは、画像系列の背景に関する低次元の多様体を生成モデルで抽出することで、背景のモデルを生成する。

アルゴリズムは差分画像の計算から始まると考えれば、この生成モデルの深層アーキテクチャもわかり易い構成になる。多くの場合、差分画像の計算結果には、疎らな外れ値が残る。確かに時系列的に隣り合う二つのフレームの差分画像を計算すれば、その計算結果には、移動体の痕跡も描かれている。しかしそれ以外にも、この差分画像には移動体の影や照明の変化も含まれている。NUMODのモデルは、こうした影や照明から移動体を識別するために、影と照明不変表現(illumination invariant representation)を事前知識として導入している。この関連からNUMODは、この照明不変表現に基づいて、誤差関数に幾つかの制約を追加している。これにより、各差分画像の疎な部分を「照明」と「前景」に分解する。

スケール不変特性

Bahri, F., et al.(2018)は、Chen, L. H., et al.(2011)に倣い、照明不変表現をウィナーフィルタの拡張系によって抽出している。Chen, L. H., et al.(2011)によれば、自然画像はアトランダムに生成された画像とは異なる幾つかの特徴を持つ。その一つが「スケール不変(Scale Invariance)」の特性である。

従来の方法では、こうした特徴はスペクトルの高周波部分に潜在化していると想定されていた。だがそうして照明のスペクトルのモデル化に注視した場合に盲点となるのは、反射率のモデル化である。この関連からChen, L. H., et al.(2011)は、自然画像のパワースペクトルを解析することにより、スケール不変の特徴の一部が低周波部分にも潜在化していることを明らかにしている。低周波数帯域には、フーリエ領域のべき乗則の観点から、反射率の情報の一部も含まれているのである。

そこでChen, L. H., et al.(2011)は、照明不変の特徴を画像からより良く分離するためのウィナーフィルタを設計している。ここで仮定されるのは、画像の特徴に備わるべき乗則スペクトルと定常信号である。スペクトルを二つの異なるべき法則から分離するためには、照明用に低周波をカットアウトしても、あるいは信号を低周波空間に投影することで照明の情報を取得しても、不十分である。あくまでもスペクトルの全体を考慮しなくてはならない。そこでウィナーフィルタが有用となる。このフィルタリングにおいては、スペクトル領域が一般的に直線ではなく曲線として表現される。

Chen, L. H., et al.(2011)の研究では、スケール不変特性を利用することで、照明の情報を画像から分離できる範囲が調査されている。例えば顔のカテゴリでは、この類の分離は、認識率に応じて、他の最先端の照明不変の特徴抽出方法よりも優れた結果を出している。

高周波と低周波の差異

この関連からBahri, F., et al.(2018)は、照明の変動に対してロバストな自然画像のべき乗測スペクトルの仮定から導入されたShakeri, M., & Zhang, H. (2016)のウィナーフィルタを採用している。Shakeri, M., & Zhang, H. (2016)のウィナーフィルタは、周波数スペクトルの全体に渡って、照度と反射率をより良く分離する識別的な方法として設計されている。このフィルタリングは、たとえ夜間の暗い画像を観測していた場合でも、その後の激しい照明の変化に対してロバストであり続けられる。ただしこのフィルタによって得られた表現は、色度を喪失させるために、Shakeri, M., & Zhang, H. (2016)のモデルでは、元の画像の対数色度を維持するためのエントロピー最小化に基づく影の除去法を利用している。

Shakeri, M., & Zhang, H. (2016)の提案を要約して言えば、ウィナーフィルタは、自己相関関数が異なる二つの与えられた発生源から生成された二つの信号の合計を分解する。ここで、自己相関関数のフーリエ変換は、パワースペクトル密度に対応する。この方法では、全ての周波数において特徴が保持される。だが多くの周波数領域の解析方法では、専ら高周波の特徴ばかりが保持される。一方、多くの有意味な情報は、低周波の特徴として保持される。ここに、照明不変表現の鍵がある。ウィナーフィルタは、二つの信号によって構成された複合的な信号における二つのスペクトルを分解するために、ベイヤーフィルター(Bayer filter)として機能する。そのため、このフィルターに画像を観測させれば、画像の照明不変表現が抽出される。

NUMODのネットワーク構造

以下の関数は、入力画像を照明不変表現へ変換していることを示している。

$$I_i^{inv} = \phi(I_i) \tag{1}$$

ここで、$$I_i \in R^m, i = 1, 2, …, n$$は、n個の要素から成るベクトル化されたRGBの入力画像の系列を表す。以下のように、NUMODはこの入力画像を三つの変数に分解する。

$$I_i = B_i + C_i + F_i \tag{2}$$

ここで、$$B_i, C_i, F_i$$はそれぞれ背景情報、照明変化情報、そして移動体を表す。下図に要約される通り、背景画像$$B_i$$は低次元の入力ベクトル$$U_i^1$$を観測したニューラルネットワークの生成モデルによって生成される。

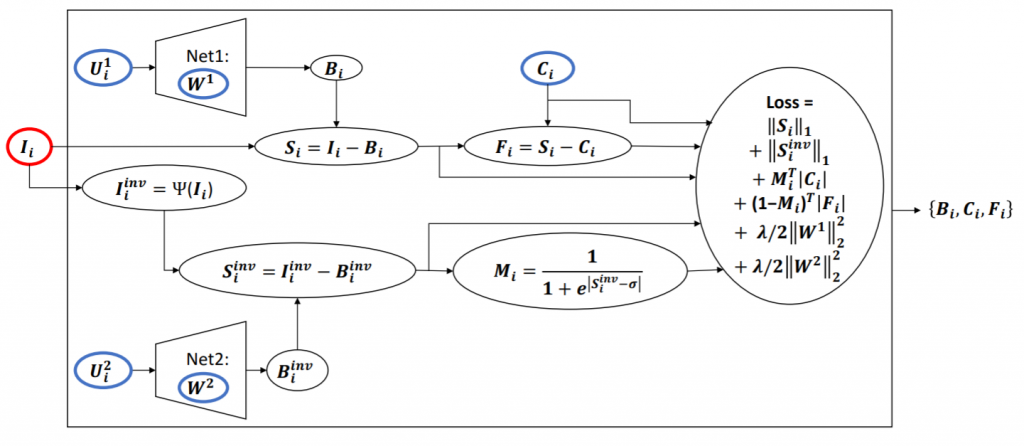
Bahri, F., Shakeri, M., & Ray, N. (2018). Online illumination invariant moving object detection by generative neural network. arXiv preprint arXiv:1808.01066., p4.

生成モデルとしては、Net1とNet2という二つのアーキテクチャが配備されている。一方は背景画像それ自体の生成を担い、他方は背景画像の照明不変表現の生成を担う。二つの生成モデルの入力ベクトル$$U_i^1, U_i^2$$と、照明変化情報となる$$C_i$$は、共にこのネットワーク構造では最適化可能なパラメタとして扱われる。照明不変特性を適用することで、$$C_i$$は、$$F_i$$と共に、$$I_i – B_i$$から得られる疎なベクトルを変換することで得られる。

自己符号化器と生成モデルの差異

Bahri, F., et al.(2018)も認める通り、生成モデルのネットワーク構造は自己符号化器(Auto-Encoder)の復号化器(Decoder)のそれと類似している。確かに誤差関数の第三項は、生成モデルの出力が生成モデルの入力に近しいか否かの値となっている。自己符号化器では、低次元の潜在的な多様体は符号化器(Encoder)によって学習される。しかしBahri, F., et al.(2018)の生成モデルでは、最適化可能なパラメタとして位置付けられている。学習中、この生成モデルは入力分布の低次元多様体を潜在ベクトルとして学習する。これ以上の制約が適用されない場合、ネットワークは単純な恒等関数を学習する。

このように述べるBahri, F., et al.(2018)は、多様体仮説の関連からGoodfellow, I., Bengio, Y., & Courville, A. (2016)を参照している。しかし、当のIan Goodfellowは、生成モデルと自己符号化器の差異をそれほど重視してはいないように見受けられる。例えばMakhzani, A., Goodfellow, I., et al. (2015)で提案されている「敵対的自己符号化器(Adversarial autoencoders)」の理論は、「自己符号化器を生成モデルへ変換することができる」(Makhzani, A., Goodfellow, I., et al., 2015, p1.)。

Bahri, F., et al.(2018)のNet1とNet2を自己符号化器として構造化した場合、設計者はより多くの可能性を手にする。例えばNet1を自己符号化器として構造化させ、この自己符号化器にアトランダムにサンプリングされた画像を入力した場合を想定してみよう。この場合、潜在ベクトルから学習していく生成モデルに比べて、自己符号化器は、入力の時点で背景画像に直結した画像を観測することができる。入力された画像には、背景についての多くの情報が埋め込まれているはずだ。それ故、再構成誤差最小化によって、自己符号化器は、単なる生成モデルに比べて多くの情報を入手した状態から背景画像を推論することができる。

「敵対的自己符号化器」のような理論は、生成モデルと自己符号化器を代替可能にすることで、この二つの概念の区別を棄却することを可能にしてくれる。この観点から観れば、NUMODはむしろ自己符号化器との接続によって拡張されるポテンシャルを秘めていることがわかる。これについては、別の機会に取り上げる。

参考文献

• Bahri, F., Shakeri, M., & Ray, N. (2018). Online illumination invariant moving object detection by generative neural network. arXiv preprint arXiv:1808.01066.
• Braham, M., & Van Droogenbroeck, M. (2016). Deep background subtraction with scene-specific convolutional neural networks. In IEEE International Conference on Systems, Signals and Image Processing (IWSSIP), Bratislava 23-25 May 2016 (pp. 1-4). IEEE.
• Chen, L. H., Yang, Y. H., Chen, C. S., & Cheng, M. Y. (2011, June). Illumination invariant feature extraction based on natural images statistics—Taking face images as an example. In CVPR 2011 (pp. 681-688). IEEE.
• Goodfellow, I., Bengio, Y., & Courville, A. (2016). Deep learning (adaptive computation and machine learning series). Adaptive Computation and Machine Learning series, 800.
• Makhzani, A., Shlens, J., Jaitly, N., Goodfellow, I., & Frey, B. (2015). Adversarial autoencoders. arXiv preprint arXiv:1511.05644.
• Shakeri, M., & Zhang, H. (2016). Illumination invariant representation of natural images for visual place recognition. In 2016 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS) (pp. 466-472). IEEE.
• Xu, P., Ye, M., Li, X., Liu, Q., Yang, Y., & Ding, J. (2014, November). Dynamic background learning through deep auto-encoder networks. In Proceedings of the 22nd ACM international conference on Multimedia (pp. 107-116). ACM.
• Yang, B., & Zou, L. (2015). Robust foreground detection using block-based RPCA. Optik-International Journal for Light and Electron Optics, 126(23), 4586-4590.