問題再設定:再構成誤差最小化問題としてのラベルノイズ問題
ニューラルネットワーク最適化問題としてのラベルノイズ問題で取り上げたように、機械学習の分類問題において、「ラベルノイズ(label noise)」は重要な派生問題になる。識別モデルの教師データとしてラベル付きサンプル(labeled samples)を用意する場合、ラベルを付与するのは、大抵の場合は人間となる。ラベルノイズという概念は、こうした人間によるラベル付けに起因した識別モデルの攪乱要因として位置付けられている。例えば一部のサンプルにのみ誤ったラベル付け(miss labeling)を施してしまえば、それは、予測精度の低下や必要な訓練データ数の増大など、分類の性能に対して多くの潜在的な悪影響を及ぼす。
Frénay, B., & Verleysen, M. (2013)らのラベルノイズ問題(Label noisy problem)では、ミスラベリングの問題が3つに区別されている。
- ラベルそれ自体の分布からも、データの分布からも独立した完全にアトランダムなノイズ(noisy completely at ranodom)。この場合、ミスラベリングという事象は一様分布に条件付けられて生起する。
- データに対して独立で、ラベルそれ自体の分布には独立したアトランダムなノイズ(noisy at random)。
- ラベルそれ自体の分布からも、データの分布からも、条件付けられて生起するアトランダムではないノイズ(noisy not at random)。
2.の例は医療分野の、特に被験者のバイタルデータなどのように、ラベルを入手すること自体に困難さが伴い、しばしば厳密なラベリングができない場合に該当する。3.の例は、異なるラベルのように思えても、データの特徴点の類似性が高い場合に該当する。例えば猫と犬の識別よりも、猫と山猫の識別のほうが、このミスラベリングは生起し易い。
ニューラルネットワーク最適化問題としてのラベルノイズ問題では、このラベルノイズ問題を専らニューラルネットワーク最適化問題として記述した。しかし、特に2014年から2018年にかけて、Auto-Encoderが広く注目を集めるようになってからは、このニューラルネットワーク最適化問題は、再構成誤差最小化問題として具象化されるようにもなっている。丁度Auto-EncoderやEncoder/Decoderを異常検知モデルとして機能させるEncDec-ADのフレームワークが想定するように、再構成誤差最小化問題におけるラベルノイズは、Auto-Encoderが観測する外れ値(outlier)のラベルとして定式化される。
問題解決策:識別的再構成誤差最小化の学習アルゴリズム
Xia, Y., et al. (2015)は、ラベルなしサンプルの学習を可能にするAuto-Encoderの機能に着目することで、「識別的再構成(discriminative reconstructions)」による教師なしのラベルノイズ除去法を提案している。その基礎概念は端的に次の一文に表れている。
「正データの再構成誤差は、常に外れ値の再構成誤差よりも小さくなる。」
Xia, Y., Cao, X., Wen, F., Hua, G., & Sun, J. (2015). Learning discriminative reconstructions for unsupervised outlier removal. In Proceedings of the IEEE International Conference on Computer Vision (pp. 1511-1519)., p1512.
実際、この現象はAuto-Encoderの性質に起因している。Auto-Encoderがノイズの多いデータを低次元の多様体表現に圧縮する場合、低次元の中間層が情報のボトルネックのように機能するために、全てのデータを適切に再構成することは原理的にあり得なくなる。情報のボトルネックを前提とした場合、一つ一つのラベル付きサンプルを完璧に再構成するのではなく、総体的に観た場合の再構成誤差を最小化していく戦略を採らざるを得ない。そのためにAuto-Encoderは、訓練データ集合の統計的な規則性を捕捉できる表現を発見しなければならない。ノイズの少ない正データの分布は、ノイズの多いデータの分布に比して規則的だ。したがって、正データの分布は上手く再構成される可能性が高い。その結果、正データの再構成誤差は比較的低くなる。
念のため補足しておくと、以上のようなXia, Y., et al. (2015)の発想に例外があり得るとすれば、Auto-Encoderの特徴写像が恒等写像になる場合だ。だがその場合は、正則項を与えることで回避することができる。低次元の中間層が情報のボトルネックとして機能するという想定は覆らない。
Xia, Y., et al. (2015)は以上のようなAuto-Encoderの構造を前提とした上で、Auto-Encoderの再構成誤差最小化の学習アルゴリズムとして実行される確率的勾配降下法に着目する。Auto-Encoderの誤差関数と勾配は次のように計算される。
$$\mathcal{J}(f) = \frac{1}{n}\sum_{i=1}^n\epsilon_i = \frac{1}{n}\sum_{i=1}^{n}\mid\mid f(x_i) – x_i\mid\mid^2$$
$$\bar{g} = \frac{d\mathcal{J}}{d\mathcal{f}} = \frac{1}{n}\sum_{i=1}^{n}g_i = \frac{2}{n}\sum_{i=1}^{n}\left((f(x_i) – x_i\right)$$
ここで、$$x_i$$はバッチサイズnの観測データ点を表し、fは符号化(encoder)と復号化(decoder)から成る再構成の特徴写像を表わす。Auto-Encoderが学習した場合、上記の勾配は全訓練データの平均に対応する。したがって、個々のデータ点について言えば、総体的な勾配$$\bar{g}$$は、個々のデータ点の勾配$$g_i$$から区別される。このことは、Auto-Encoderが全ての単一データ点の再構成誤差を最小化しようとしているのではなく、総体的な再構成誤差を最小化しようとしていることを意味する。
Auto-Encoderの学習によって個々のデータ点の再構成誤差がどの程度最小化されているのかを知るには、有効勾配強度(effective gradient
magnitude)、つまり各データの勾配の方向への総体的な勾配の投射(projection)によって測定できる。
$$g_i^{effect} = \frac{<g_i, \bar{g}>}{\mid g_i \mid} = \mid \bar{g} \mid \cos \theta (g_i, \bar{g})$$
ここで、$$\theta (g_i, \bar{g})$$は総体的な勾配と各データ点の勾配の角度を表わす。
ノイズの多い訓練データ集合では、総体的な勾配は正データによって支配される可能性が高い。外れ値は通常実際のタスクにおける正データほど多くはない。仮に外れ値がたとえデータ集合の半分以上を占めていたとしても、正データは依然として勾配を支配する可能性がある。何故なら、外れ値が特徴空間全体に任意に分散していたとしても、その結果、勾配方向は相殺されるためだ。一方、正データは密に分布している。その勾配方向は比較的一貫している。尤も、ノイズの多い訓練データ集合に多くの外れ値がある場合には、流石に正データは支配的な位置を占めることができない。
正データが総体的な勾配の方向を支配している場合、正データの勾配と総体的な勾配の角度は、外れ値データの勾配と総体的な勾配の角度よりも小さくなる。それは結果的に、上述した有効勾配強度$$g_i^{effect}$$の値を大きくする。言い換えれば、総体的な勾配は、正データの再構成誤差を最小化することにより多くの影響力を有するようになる。したがって、ノイズの多いデータで訓練されたAuto-Encoderは、正データをより良く再構成する可能性が高くなる。
問題解決策:Label-denoising Auto-Encoder
Xia, Y., et al. (2015)のモデルは、あくまでラベルなしサンプルの外れ値を除去することを目指したモデルである。そのため厳密に言えば、このモデルはラベルノイズ問題への解決策として機能しない。しかしラベルノイズ問題に対するAuto-Encoderのモデリングは、基本的に再構成誤差最小化の学習アルゴリズムによって、「外れ値」としてのラベルノイズを発見探索していくことが可能になるという前提に立っている。
Wang, D., & Tan, X. (2014)のLabel-denoising Auto-Encoderは、入力されたサンプルとラベルのt-hotベクトルを横方向に結合した行列を観測データ点として観測する。そして、denoising Auto-Encoderのアルゴリズムにより、誤差の最小化による学習を実行する。ただしここでの誤差は、通常のAuto-Encoderとは異なり、単なる再構成誤差ではない。誤差関数は次のような再構成誤差と分類誤差の複合体となる。
$$\min_{W\theta} \lambda J(X, W) + (1 – \lambda) J(\tilde{Y}, \theta) + \gamma \mid\mid W \mid\mid^2 + \beta \mid\mid \theta \mid\mid^2$$
$$J(X, W) = \sum_{i=1}^n \mid\mid \hat{x}_i – x_i \mid\mid^2$$
$$J(\tilde{Y}, \theta) = – \sum_{i=1}^n\sum_{k=1}^K \mathbf{1}\{\tilde{y}_i = k\} \cdot \log \hat{y}_{ik}$$
ここで、$$X$$はラベル付きサンプル$$x_i$$を有した訓練データセットを表す。$$W$$と$$\theta$$はそれぞれ再構成誤差最小化と分類誤差最小化のパラメタを表す。$$0 \leq \lambda \leq 1$$は二つの誤差のトレードオフパラメタを表す。$$\gamma$$と$$\beta$$はそれぞれ重み減衰ないしL2正則化の重み付けを表す。$$\tilde{y}_i$$と$$\hat{y}_i$$はそれぞれ破損されているラベルのベクトルと再構成されたラベルのベクトルを表す。最後に、このAuto-Encoderは$$x_i$$も再構成する。これを$$\hat{x}_i$$と表記している。
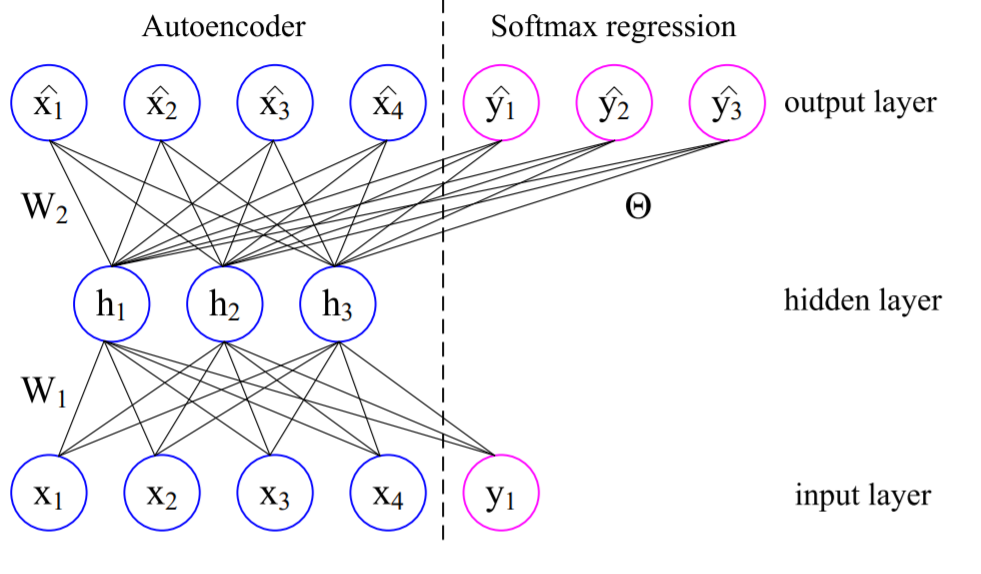
Wang, D., & Tan, X. (2014, August). Label-denoising auto-encoder for classification with inaccurate supervision information. In 2014 22nd International Conference on Pattern Recognition (pp. 3648-3653). IEEE., p3650より。
注目すべきは、このノイズ除去型の再構成データの形式である。3層のAuto-Encoderを仮定するなら、順伝播により、$$\hat{x}_i$$は次のように計算される。
$$\hat{x}_i = S(W_2 \times S(W_1 \times [x_i, \tilde{y}_i] + b_1) + b_2)$$
ただし、$$S$$はシグモイド関数を表す。
このように、$$\hat{x}$$は$$[x_i, \tilde{y}_i]$$の組み合わせに依存して計算される。
一方、$$\hat{y}_{ik}$$は、次のように推定される。
$$\hat{y}_{ik} = C \times \exp (\theta_k \times S(W_1 \times [x_i, \tilde{y}_i] + b_1)$$
ここで、$$\theta_k$$は出力層における$$k$$次元のパラメタベクトルを表す。$$C$$は規格化定数で、これにより$$\sum_k^{}\hat{y}_{ik} = 1$$が保証される。
問題解決策:Class-Specific Autoencoder
Wang, D., & Tan, X. (2014)のLabel-denoising Auto-Encoderで想定されるサンプルは、ラベルを表わすt-hotベクトルと横方向に結合する都合上、t-hotベクトル同様に、rank-2の行列で構成されていなければならない。そのため、ラベル付きサンプルがConvolutional Auto-Encoderで想定される画像データやLSTM based Encoder/Decoderで想定される時系列データである場合には、直ぐにこのモデルを利用することはできなくなる。特に入力が画像データとなる場合には、サンプルとラベルのt-hotベクトルを単純に結合することができない。もし経験的に入力データが畳み込みや回帰的ネットワークで表現するべきであると仮定できる場合には、別のAuto-Encoderをモデル化しなければならなくなる。
これに対して、Zhang, W., et al. (2018)やZhang, W., et al. (2019)は、ラベルノイズが含まれている観測データ点を外れ値として処理するClass-Specific Autoencoderをモデル化することで、原理的に如何なるAuto-Encoderでも構成可能なラベルノイズ対策を展開している。彼らのモデリングは非常に単純な発想に基づいている。それは、観測データ点を予めラベルごとに区別した場合、各ラベルに対応するラベル付きサンプルのうち、ラベルノイズが含まれているラベル付きサンプルは、相対的に外れ値になり得るという発想である。それ故Zhang, W., et al. (2018)らは、再構成誤差最小化問題をラベルごとに解く次のような定式化を試みている。
$$\newcommand{\argmin}{\mathop{\rm arg~min}\limits} y_t = \argmin_{j=1, 2, 3, …, K} \mid\mid g_j(f_j(x_t)) – x_t\mid\mid^2$$
ここで、jはK個から成るラベルの番号を表わす。$$x_t$$は予めラベルtとしてラベリングされていたラベルtのサンプルを表わす。$$f_j$$はラベルjにおける符号化(encode)を、$$g_j$$はラベルjにおける復号化(decode)を、それぞれ表す。そして、$$y_t$$はラベルノイズを考慮したラベルのラベル番号であるということになる。もしラベルノイズが全く無いか、もしくは相対的に最も少ない場合、ラベル付け担当者が想定する$$x_t$$のラベルと$$y_t$$が指し示すラベルは一致するはずだ。一方、双方が一致しない場合、$$y_t$$はラベル付け担当者が想定しなかった別様のラベルを意味する。
符号化(encode)と復号化(decode)には、単純な多層のニューラルネットワークのみならず、Auto-Encoderとして構造化できる関数ならば原理的に何を代入しても良い。符号化に畳み込み層を導入したのなら、復号化には転置畳み込み(Transposed convolution)層を導入すれば良い。また、上式は再構成の誤差関数に平均二乗誤差(Mean Square Error: MSE)を導入している。だがこれに従う必然性も無い。別の誤差関数を導入しても良く、また正則項を加えても良い。この観点で観れば、Wang, D., & Tan, X. (2014)のモデルに比して、Zhang, W., et al. (2018)らのモデルは機能的な拡張性が高い。
問題解決策:label cleaning network
Xia, Y., et al. (2015)の識別的再構成誤差最小化の学習アルゴリズムは、ラベルなしサンプルを対象としたAuto-Encoderのみで実現するために、少ないサーバーリソースと実装コストで実用化することができる。だがその効果は、教師なし学習であるが故に、限定的かつヒューリスティックで留まってしまう。一方、Zhang, W., et al. (2018)らのモデリングは、ラベルごとにAuto-Encoderのパラメタ、順伝播、誤差関数を導入することになる。そのためこのモデルを実装する場合、ラベル数に比例してメモリ負荷を高めてしまうことになる。こうしたスケーラビリティとラベルノイズ対策としての効果との間で伴うトレードオフを対処するには、可能な限り少ないモデルによって、より多くのラベル数を対象としたラベルノイズ対策を可能にしなければならない。
Lee, K. H., et al. (2018)は、label cleaning networkを導入することで、このトレードオフに相対している。このネットワーク構造においては、Auto-Encoderのencoder部分が、Reference set encoderとQuery Encoderに区別される。Reference set encoderは、一つのラベルにおいて参照される観測データの集合を「注意機構(attention mechanism)」によって符号化することで、その「ラベルを表現した埋め込みベクトル」を出力する。一方、Query Encoderは、個々の観測データについてのクエリの埋め込みベクトルを計算する。このQuery encoderは、各クエリがそのラベルに関連している場合に、そのクエリを表現した埋め込みベクトルがその「ラベルを表現した埋め込みベクトル」に類似するように制約を課す。
言い換えればこのモデルは、クエリの埋め込みベクトルとラベルの埋め込みベクトルとを比較することで、観測データのラベルが誤っているか否かを判断できるようになる。異なる参照集合から生成されたラベルの埋め込みは、モデルを適合させようとしている異なるラベルを表わす。そのためこのlabel cleaning networkは、明示的な人間の教師データなしに、ラベルを一般化することができる。
Reference set encoder$$f_s(\cdot)$$は、特定のラベルに対して収集されたノイズのある参照データセットの代表的な特徴に焦点を当てることを学習することで、ラベルを表現した埋め込みベクトルを出力する。参照集合内の全てのデータを利用する場合、計算コストが高まる。そのため、最初に代表的なサブ集合を作成した上で、そのサブ集合内の各データから一つの視覚的な特徴ベクトルを抽出することにより、代表的な特徴ベクトル集合を形成する。ここで、ラベルcの代表的な参照特徴ベクトル集合を$$V_c^s$$と置く。この参照特徴ベクトル集合は、ランダムにサンプリングされるか、K-Means法のようなデータ・クラスタリングによって抽出される。
$$f_s(\cdot)$$と並行して、Query encoderを$$f_q(\cdot)$$とする。ここで、qはcのラベルが付与されたクエリデータを表わす。$$f_q(\cdot)$$はクエリデータの特徴$$v^q = f_v(q)$$を写像することで、クエリを次のように埋め込む。
$$\phi^q = f_q(v^q)$$
label cleaning networkは、qがラベルcと関連する場合に、このクエリの埋め込みベクトルを次のラベルを表現した埋め込みベクトルに類似するように訓練される。
$$\phi_c^s = f_s(V_c^s)$$
言い換えれば、label cleaning networkは、一定の$$\phi_c^s$$を比較の観点として固定した上で、複数のクエリに対応した$$\phi^q$$を比較していくのである。
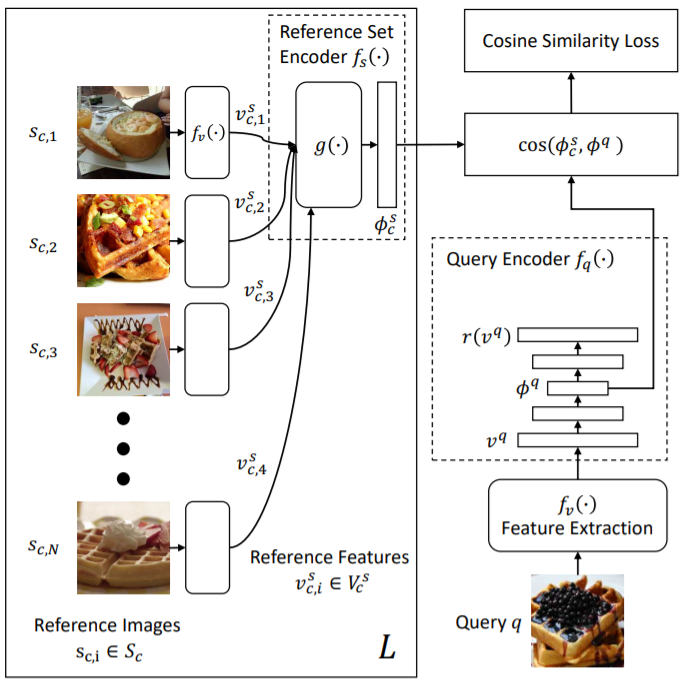
Lee, K. H., He, X., Zhang, L., & Yang, L. (2018). Cleannet: Transfer learning for scalable image classifier training with label noise. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (pp. 5447-5456)., p5448より.
ラベルにはノイズが多い。そのため、クエリデータとそのラベルノイズを手動で付与した「検証ラベル(verification label)」によって、そのノイズをマークアップすることができる。検証ラベルlは、データがそのノイジーなラベルと対応している場合には1を、データが誤ってラベル付けされている場合には0を、そして検証ラベルがそもそも利用不可能な場合には-1と、形式的に定義される。ラベル付け担当者となる人間のコストを削減するためには、ほとんどの検証ラベルは-1となる。
Reference set encoder$$f_s(\cdot)$$は、まず二層のニューラルネットワークによって、隠れ層$$h_i$$を表現する。次に、以下のような注意機構により、参照集合の注目に値する特徴を表現する。
$$u_i = \tanh (Wh_i + b)$$
$$\alpha_i = \frac{\exp(u_i^Tu)}{\sum_{i}^{}\exp(u_i^Tu)}$$
$$h = \sum_{i}^{}\alpha_ih_i$$
ここで、uは「文脈ベクトル(context vector)」を表わす。uは学習を通じて更新される。またhが表しているのは、$$u_i$$と文脈ベクトルuの類似性である。
このようなマッチング制約によって駆動されるこの注意機構は、ラベルの最も代表的な関数に注意を払う方法を学習する。
一方、Query encoderは五層のAuto-Encoderによって構成される。このAuto-Encoderは、検証ラベルの無いラベルを含む全てのラベルの意味論的な情報をクエリの埋め込みに強制的に保存する。
クエリの特徴ベクトルを$$v^q$$とするなら、このAuto-Encoderは$$v^q$$を隠れ表現$$\phi^q$$を写像すると共に、$$\phi^q$$から$$v^q$$を再構成する。このAuto-Encoderが最小化すべき再構成誤差は次のようになる。
$$L_r(v^q) = \mid v^q – r(v^q)\mid^2$$
ここで、rは再構成の関数を表わす。
ラベルを表現した埋め込みベクトルと個々のデータを表現した埋め込みベクトルとのマッチング制約は、以上の二つのAuto-Encoderの学習を前提としている。人間の検証ラベルからの監督により、ラベルの埋め込みベクトルとデータの埋め込みベクトルとの類似性は、検証ラベルlが1の場合には最大化され、検証ラベルlが0の場合には最小化され、検証ラベルlが-1の場合には形式的に0と定義せざるを得なくなる。
一方、検証ラベルの無いデータに対しても、検証ラベルなしのデータに類似した検証を適用する教師なしの自己補強戦略を適用したマッチング制約を学習するために利用することができる。
参考文献
- Lee, K. H., He, X., Zhang, L., & Yang, L. (2018). Cleannet: Transfer learning for scalable image classifier training with label noise. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (pp. 5447-5456).
- Xia, Y., Cao, X., Wen, F., Hua, G., & Sun, J. (2015). Learning discriminative reconstructions for unsupervised outlier removal. In Proceedings of the IEEE International Conference on Computer Vision (pp. 1511-1519).
- Zhang, W., Wang, D., & Tan, X. (2018, June). Data cleaning and classification in the presence of label noise with class-specific autoencoder. In International symposium on neural networks (pp. 256-264). Springer, Cham.
- Zhang, W., Wang, D., & Tan, X. (2019). Robust Class-Specific Autoencoder for Data Cleaning and Classification in the Presence of Label Noise. Neural Processing Letters, 50(2), 1845-1860.
- Wang, D., & Tan, X. (2014, August). Label-denoising auto-encoder for classification with inaccurate supervision information. In 2014 22nd International Conference on Pattern Recognition (pp. 3648-3653). IEEE.