問題設定:統計的因果探索問題
ベイジアンネットワークの構造学習は、既知の事象ばかりがノードとして参照される傾向にある。既知の事象同士の因果推論を実践する場合、この制約は有害ではない。一方、未知の事象も含めた因果探索を実践する場合、この制約は有害となる。
未知の事象は、LiNGAMの理論でも想定されていた通り、潜在変数として記述できる。ベイジアンネットワークの構造学習が潜在変数を扱う場合、潜在変数を特定して記述するだけではなく、その離散化も施さなければならない。
実務上、この離散化は、データのカテゴリ化によって実践される。しかしながら、そのカテゴリが未知であるからこそ、未知の事象は潜在変数なのである。この潜在変数を観察しようとする多くの実務家たちは、未知のカテゴリを探索するアルゴリズムとして「データクラスタリング(data clustering)」を採用する傾向にある。データクラスタリングとは、人間によってアノテーションが付与されたラベル付きサンプルではなく、ラベルなしサンプルを分割することによって、データを自動的に分類していく手法である。
しかし、データクラスタリングによって分類されたカテゴリは、通常人間にとっては直感的にわかり難いデータとなる。データクラスタリングによって抽出されたクラスタが何を意味し、どのようなデータセットを代表しているカテゴリであるのかがわからなければ、そのクラスタリング結果をノードとして運用することは難しくなる。
問題解決策:確率的潜在的意味解析
自然言語処理やテキストマイニングの分野では、こうした直感的に理解し難いクラスタに「意味(semantic)」を付与する統計的な問題解決策が導入されている。いわゆる「確率的潜在的意味解析(Probabilistic Latent Semantic Analysis: PLSA)」は、文書に含まれる潜在的な「トピック(topic)」を抽出する手法として知られている。各文書のトピックは、必ずしもその文書の単語集合上で明示的に指示されている訳ではない。暗示や皮肉、比喩や隠喩など、ハイコンテクストな会話では、しばしばトピックが明示されない。こうした隠れたトピックを特に「潜在的トピック(latent topic)」と呼ぶ。同様に、ある文の単語の意味は、その周辺で共起している単語との構文論的あるいは意味論的な関連によって規定される。こうした各単語の意味は、当の単語それ自体が指し示している訳ではない。こうして必ずしも明示されない意味を「潜在的意味(latent semantics)」と呼ぶ。潜在的トピックは、この「潜在的意味」のクラスタを意味する。
潜在的ディリクレ配分法
潜在的トピックを抽出する初歩的な統計モデルの一つは、「潜在的ディリクレ配分法(Latent Dirichlet Allocation: LDA)」として知られている(Blei, D. M., Ng, A. Y., & Jordan, M. I., 2003)。LDAは確率的な生成モデルの一種で、機械学習というよりは統計的機械学習問題の枠組みで導入される傾向がある。$$N$$個の用語によって構成される$$D$$個の文書集合によってコーパスが生成される時、このコーパスには合計$$K$$個のトピックが埋め込まれている。この場合、LDAは次のような三段階の生成モデルになる。
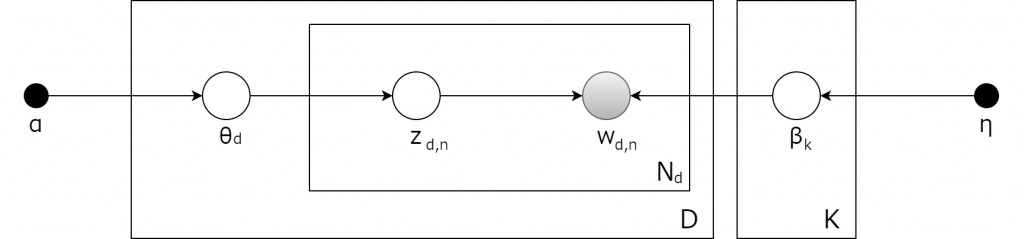
上記のグラフィカルモデルでは、各ノードは確率変数を表わし、生成過程を担っている。白背景のノードは可視変数で、灰色のノードは潜在変数を表わす。この場合、コーパス内の用語は観測された用語に限定される。つまり、用語の生成は別様にもあり得る。
潜在変数は次の2点を規定する。
1. コーパス内のトピックの確率的な混合
2. 各文書における各用語の頻度分布
LDAの統計モデルとしての機能は、観測された用語から潜在的トピックの構造を推定することにある。LDAでは、各文書が複数の用語のみならず複数のトピックからも構成されるという想定から、トピックの構成比率を離散分布として獲得することを目指している。この関連から、LDAのモデリングの基礎となる確率分布には、多項分布の共役事前分布となるディリクレ分布が採用される。
潜在的ディリクレ配分法のアルゴリズム
$$\theta$$をパラメタとするディリクレ分布を$$Dirichlet(\theta)$$と表わす。コーパスをモデル化する時、LDAのモデルは、コーパスに対して次のような生成過程を想定することになる(Hoffman, M., Bach, F., & Blei, D., 2010)。
1. それぞれのトピック$$k \in K$$ごとに、$$\beta_k \sim Dirichlet(\eta)$$をサンプリングする。これは、トピック$$k$$における用語の発生確率に照応した用語の分布となる。$$\eta$$はそれぞれのトピックにおける用語の事前分布を成す。
2. それぞれの文書$$d \in D$$ごとに、トピックの構成比率として、$$\theta_d \sim Dirichlet(\alpha)$$をサンプリングする。ここで、$$\alpha = (\alpha_1, …, \alpha_l)$$は$$l$$次元ベクトルで、ディリクレ分布のパラメタを表わす。
3. 文書$$d$$の用語$$i$$において、
1. トピックの配分$$z_{di} \sim Multinomial(\theta_d)$$をサンプリングする。
2. 観測された用語$$w_{ij} \sim Multinomial(\beta_{z_{di}})$$をサンプリングする。
事後分布
パラメタ推定において、事後分布は次のようになる。
$$p(z, \theta, \beta \mid w, \alpha, \eta) = \frac{p(z, \theta, \beta \mid \alpha, \eta)}{p(w \mid \alpha, \eta)}$$
しかし、右辺は扱い難いため、変分ベイズ法により、より単純な分布$$q(z,\theta,\beta | \lambda, \phi, \gamma)$$を近似として扱う。これらの変分パラメタ$$\lambda, \phi, \gamma$$は、変分下限(evidence lower bound: ELBO)の最大化として最適化される。この最大化問題の枠組みは$$q(z,\theta,\beta)$$と真の分布$$p(z, \theta, \beta |w, \alpha, \eta)$$のカルバックライブラーダイバージェンス(Kullback-Leibler(KL) divergence)の最小化問題と等価になる。
$$\log\: P(w | \alpha, \eta) \geq L(w,\phi,\gamma,\lambda) \overset{\triangle}{=}E_{q}[\log\:p(w,z,\theta,\beta|\alpha,\eta)] – E_{q}[\log\:q(z, \theta, \beta)]$$
変分推論、あるいは変分ベイズ法
KLダイバージェンス最小化問題への再設定は、決して突飛な発想などではない。背景にあるのは、「変分推論(variational inference」、あるいは「変分ベイズ法(Variational Bayesian method)」と呼ばれるパラメタの分布推定法である(Hoffman, M. D., et al., 2013)。
独立な確率変数の集合$$X = \{X_1, …, X_n \}$$の確率密度関数が$$q(x)$$とする場合、事前分布$$\phi(\theta)$$と統計モデル$$p(x \mid \theta)$$の周辺尤度は次のようになる。
$$Z(X) = \int \phi(\theta) \prod_{i=1}^n p(X_i \mid \theta) d\theta$$
$$\int \phi(\theta)d\theta = 1$$を満たす場合、周辺尤度が大きいほど、データに対する統計モデルと事前分布が適切となる。単なる最適化ではなく汎化誤差の最小化を目指す場合は、$$\int \phi(\theta)d\theta = \infty$$でも構わない。
変分法の機能は、事後分布$$p(X \mid \theta)$$の最も良い近似となる$$q(X)$$を求めることになる。イェンセンの不等式より、次のようになる。
$$\log p( \theta ) = \log \left( \int p( X, \theta ) \right ) dX = \log \left( \int q(X) \frac{p(X, \theta)}{q(X)}dX\right) \geq \int q(X)\log \frac{p(X, \theta)}{q(X)} dX =F(q(X))$$
この$$F(q(X))$$が変分下限となる。これを前提とすれば、変分下限と対数周辺尤度の差異は、次のように、KLダイバージェンスに照応する。
$$\log p(\theta) – F(q(X)) = \int q(X) \log p(\theta)dX – \int q(X) \frac{p(X, \theta)}{q(X)}dX = \int q(X) \log \left(\frac{p(\theta)q(X)}{p(X, \theta)}dX\right) = \int q(X) \log \left(\frac{q(X)}{p(X \mid \theta)}dX\right) = KL(q(X) \mid p(X \mid \theta))$$
参考文献
– Blei, D. M., Ng, A. Y., & Jordan, M. I. (2003). Latent dirichlet allocation. Journal of machine Learning research, 3(Jan), 993-1022.
– Heckerman, D., Geiger, D., & Chickering, D. M. (1995). Learning Bayesian networks: The combination of knowledge and statistical data. Machine learning, 20(3), 197-243.
– Hoffman, M., Bach, F., & Blei, D. (2010). Online learning for latent dirichlet allocation. advances in neural information processing systems, 23.
– Hoffman, M. D., Blei, D. M., Wang, C., & Paisley, J. (2013). Stochastic variational inference. Journal of Machine Learning Research.
– Koller, D., & Friedman, N. (2009). Probabilistic graphical models: principles and techniques. MIT press.
– 鈴木譲, 植野真臣(著)『確率的グラフィカルモデル』共立出版、2016